基于DCM模式的Buck直流变换器分动态相量法析
摘要:针对工作在DCM模式下的Buck直流变换器这个离散的、时变的、非线性系统,引入虚拟开关函数将一个开关周期中的三种电路拓扑统一到一组状态空间方程中。采用动态相量法时,合理地选择了模型中的谐波分量,讨论了虚拟开关占空比的取值,建立了其非线性、大信号、时不变模型。仿真结果表明,动态相量模型非常接近于时域模型,为设计基于大信号模型的性能优越控制器提供理论依据。
引言
动态相量法基于频率分解的思想,希望以傅里叶级数中极少量的系数来近似原始时域波形,并以这些时变的复相量为状态变量,来获得系统化的状态空间模型。它已被用于高压直流输电HVDC、TCSC、有源滤波器、电力电子变换器等系统建模分析中[1.2]。
对于电力电子变换器这个离散的、时变的、非线性系统,在采用动态向量法建模时,通常是引入开关函数,将其不同开关状态对应的电路拓扑统一到一组时域状态空间方程中。再作出相应变量的复相量,得到扩大阶数的动态相量模型。选择的变量多为电感的电流和电容的电压,通常保留其傅里叶系数的直流和基频分量。对于直流变换器,电感电流存在着CCM(Continuous Conduction Mode)和DCM(Discontinuous Conduction Mode)工作模式。在CCM工作模式下,采用动态相量法建模时能用一个开关函数将一个开关周期中两种电路拓扑统一到一组时域状态空间方程中去。由于CCM工作模式中电感电流连续,保留其傅里叶系数的直流和基频分量可以近似拟合原始时域曲线。但对于DCM工作模式下,一个开关函数无法将一个开关周期中三种电路拓扑统一到一组状态空间方程中,再者电感电流断续,其傅里叶级数频谱丰富,仅用其直流分量、基频分量较难近似拟合原时域曲线。
为了在DCM工作模式下应用动态相量法对系统进行建模分析,本文以Buck直流变换器为例,在建模时引入虚拟开关函数将一个开关周期中的三种电路拓扑统一到一组方程中。同时为保证模型的准确性,动态相量模型中保留傅里叶级数中的直流量、基频分量和二次分量,建立了Buck直流变换器DCM工作模式下的非线性、大信号、时不变模型。并给出了该模型的仿真结果。
动态相量法
在时域中x(τ)在任一区间 中的时变傅里叶级数可表示为[3]:
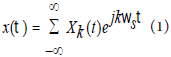
式中ωs=2π/T,Xk(t)是时变傅里叶系数,在动态相量法中定义为“相量”。不同次数的相量,可有下式得到:
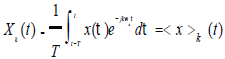 (2)
(2)式中Xk(t)是时间的函数,研究的窗(宽度为T)在x(τ)上滑动时,相量就会改变。抓住级数中重要的项,将这些相量作为状态变量,得到系统状态空间模型。
应用动态相量法有两个重要特性为:
(1)动态向量的微分特性
对于第k阶傅里叶系数,其微分形式满足:
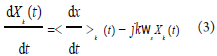
(2)相量乘积特性
两个时域变量乘积的动态相量等于每个变量所对应的动态向量的离散卷积为:
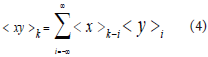
Buck直流变换器的动态向量法建模
Buck变换器电路拓扑
Buck变换器电路拓扑如图1所示,vin为直流输入电压,S1为开关,u为输出电压,i为电感L的电流。建模时做如下假定:认为S1为理想开关,VD为理想二极管;忽略电感和电容的内阻。由于变换器工作在DCM模式下,在一个开关周期内,电路有三种拓扑结构如图2所示。开关S1对应的开关函数q1波形及电感电流i的波形如图3所示。当S1闭合时q1(t)=1,当S1断开时q1(t)=0。设电感释放磁场能的时间为d2T,T为开关周期[4]。
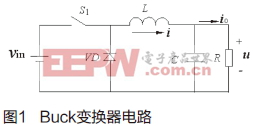


Buck变换器时域动态模型
由于在一个开关周期内,电路存在三种拓扑,仅用q1开关函数无法将三种拓扑统一到一组状态方程中去。这里引入虚拟开关S2,它对应着二极管VD的状态,对应的开关函数为q2。当VD导通时,q2(t)=1,当VD关断时,q2(t)=0,波形如图4所示。则变换器的时域状态空间方程为:


Buck变换器动态相量模型
变换器在DCM工作模式下,电感电流断续,其傅里叶级数频谱必定丰富,仅考虑其直流分量、基频分量拟合原时域中动态大信号扰动的情况,模型的准确性偏差,需考虑更多次谐波动态相量,但太多的谐波成分保留势必导致模型的复杂程度。这里选择的成分为直流分量、基频分量和二次分量。则
i和u近似表示为式(6)。由于i和u均为实数,有式(7),其中*表示复数共轭。由此可建立变换器的动态相量模型为式(8)。
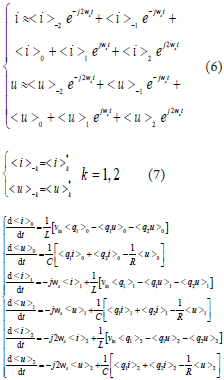 (8)
(8)模型中要保留直流分量、基频分量和二次分量,故有以下式(9)成立:对应实数形式的变换器10阶动态相量模型如下式(11),这里R表示复数的实部,I表示复数的虚部。可以看出,模型阶数增加了,但模型为一个非线性、时不变的状态空间方程。
 (9)
(9)其中
 (10)
(10)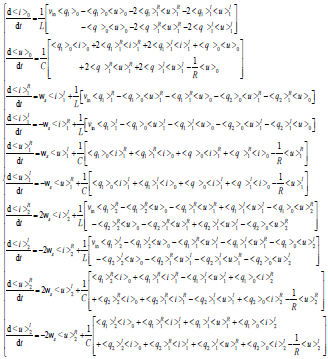 (11)
(11)Buck 直流变换器 DCM CCM 动态相量法 201308 相关文章:
- Fly-Buck 变压器是不是“新型”反激式变压器?(12-08)
- Fly-Buck 转换器 PCB 布局技巧(12-08)
- 透彻分析:电压双象限Buck-Boost电路拓扑(12-07)
- 双Buck光伏逆变器方案如何实现并网控制?(12-07)
- 基于BUCK调压的小功率高压电源(12-07)
- 以LC滤波电路的思想 玩转本安Buck变换器(12-07)
