一款基于DSP的逆变电源模糊PID控制

引言

由于逆变器传递函数不易得到，而且电压输出经常波动，传统的单纯PID控制难以达到快速和稳定的响应，而模糊控制与PID相结合的控制方法，通过对误差量的变化实时分析，调整PID参数，达到快速响应和无差跟踪，可实现逆变电源的高精度实时控制。

模糊控制系统原理

模糊PID控制器以电压偏差e 和偏差变化量ec作为输入，PID 参数模糊自整定是找出PID 三个参数与e 和ec 之间的模糊关系，在程序运行中通过不断检测e 和ec，根据模糊控制原理对三个参数进行在线修改，以满足不同e 和ec 对控制参数的不同要求，从而使被控对象有良好的动、静态性能。其在线自校正工作流程如图1所示。

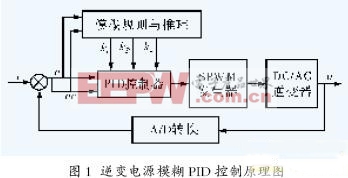
图中：ki、kp、kd分别为积分增益系数、比例增益系数和微分增益系数。

1、PID调整控制器

图1 中r 为给定参考电压，u 是逆变器实际输出电压，e 是偏差信号，ec 是偏差变化率。模拟形式的PID控制算式为

本文采用TMSLF2407实现数字PID控制，对式(1)进行离散化，可得到式(2)PID 控制的离散形式，为了增加系统的可靠性，采用增量式PID控制算式，式(2)为第k 次PID控制器的输出量，减去第k-1次PID 控制器的输出量即可得到式(3)增量式PID 控制算式。

2、模糊PID的实现

DC辕AC逆变电源控制的主要是输出电压及频率的准确性。频率的准确性由PWM发生器决定(它是一个存贮在存储器内的一个正弦输出表格)，只要触发计算准确就能达到设计要求。负载的变化使输出电流产生变化，对于一定脉宽输出的DC辕 AC电源来说，势必导致输出电压的变化。因此采用模糊控制规则根据不同的渣e渣和渣ec渣，对PID控制器的参数kp、ki、kd进行在线自整定来调节输出电压。模糊控制器的输入变量是偏差绝对值渣E渣、偏差变化率绝对值渣EC渣，模糊控制器的输出是PID 控制器的比例增益系数KP、积分增益系数KI和微分增益系数KD。本文采用CRI(Compositional Rule of Inference)推理法设计模糊规则，为了在实时控制中避免关系矩阵的合成运算，先在脱机状态下把所有可能的输入和输出情况计算出来，形成一张控制表去执行控制，控制表是以整数形式表示的，为了能产生控制表，在CRI推理法中把语言变量的论域转换成有限整数的论域，本质上是把连续论域离散后产生离散论域。采用式(5)可以将连续域离散化到整数论域N。

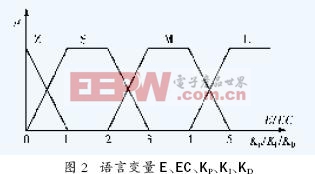
本文中，各语言变量的挡数均为4 挡(零、小、中、大)，因此取整数论域N 为{0，1，2，3，4，5，6}。此时，如图2所示，可取语言变量值4挡如下：

大(L)———取在5、6附近

中(M)———取在3、4附近

小(S)———取在1、2附近

零(Z)———取在0附近

在本文中利用CRI法推理时，控制过程是用查控制表来产生控制量的，在控制表中，模糊偏差量渣E渣、模糊偏差变化率渣EC渣，PID控制器的模糊比例增益系数KP、模糊积分增益系数KI和模糊微分增益系数KD都是用其对应整数论域的元素来表示的。对于单个实时精确量利用式(5)，得到的结果再四舍五入，就求出了对应整数论域的相应元素，从而实现了输入量的模糊化。

针对不同的e 和ec，kp，ki，kd的整定原则为：

1)当渣e渣较大时，为使系统具有较好的跟踪性能，应取较大的kp与较小的kd，同时为避免系统响应出现较大的超调，应对积分作用加以限制，通常取ki=0。

2)当渣e渣和渣ec渣中等大小时，为使系统具有较小的超调，kp应取小一些，在这种情况下，kd的取值对系统的影响较大，应取小一些，ki的取值要适当。

3)当渣e渣较小时，为使系统具有较好的稳定性能，kp和ki 均应取大些，同时为避免系统在设定值时出现振荡，并考虑系统抗干扰的性能，当渣ec渣较大时，kd可取小些;渣ec渣较小时kd可取得较大些。

根据以上整定原则和总结工程设计人员的技术知识和操作经验，建立了表1所列的模糊规则表。

式中：k 为模糊控制中对模糊量进行反模糊化时的比例因子。 3、DSP 软件算法实现

为了保证模糊PID控制的实时性和准确性，DSP在A/D采样的中断子程序中就调用模糊PID控制算法程序，立即计算出输出控制量并送到被控对象，根据TMSLF2407 的性能，机器时钟周期和中断延时可以计算出本系统从采样当前实际输出值到输出控制量大约需要6.67 滋s ，这对于1ms一次的采样来说是足够的，完全满足实时性要求。程序流程图如图3所示。

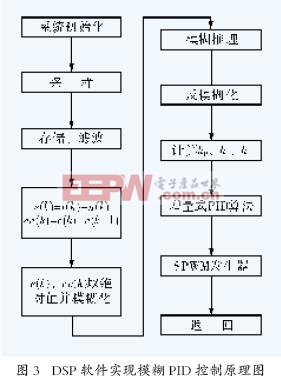
下面是部分程序。

执行PID控制

PID_Control：

SETC SXM

SETC OVM

SPM #O

LDP #4

LACL ADRESULTSACL PID_input

DALL Fuzzy_PID_table

反模糊变化程序

Fuzzy_PI_end：

LT k1

MPY Fuzzy_K

PAC

SACL Kp

LT k2

MPY Fuzzy_K

PAC

SACL Ki

LT k3

MPY Fuzzy_K

PAC

SACL K

RET

实验结果

图4为