基于FPGA的数字锁相环平台的搭建

基于锁相环的理论，以载波恢复环为依托搭建数字锁相环平台，并在FPGA中实现锁相环的基本功能。

在FPGA中实现锁相环的自动增益控制，锁定检测，锁定时间、失锁时间的统计计算，多普勒频偏的估计。

通过USB接口与电脑实现通信来交换有关锁相环的参数。电脑传递锁相环所需的参数(如等效噪声带宽等)，FPGA将锁相环的结果传递给电脑(如锁定时间，多普勒频率等)。

二、设计任务

锁相环的输入具有自动增益控制AGC模块，这样可以允许一定动态范围的信号输入，也减少了输入环路信噪比的大幅波动，从而减少了环路噪声带宽的大幅波动。

基于VHDL语言实现数字锁相环，混频基于CORDIC算法，相位提取模块是修正的反正切相位提取，环路滤波器采用理想的二阶环，NCO采用32位的累加器。设计完先进行Modelsim仿真，后利用ISE自带的CHIPSCOPE下载调试。

具有锁定检测模块，当环路锁定时，通过LED灯或数码管给出锁定指示。

通过锁定指示的输出信号，来控制一个实时时钟，这样可以统计锁定时间和失锁时间，所记录的时间存入两个FIFO。

设计USB通信模块，使得设计的锁相环可以同电脑进行通信，将接收电脑传给FPGA的环路参数，同时将检测的锁定时间和失锁时间，锁定指示，多普勒频偏估计等传输给电脑。

利用MATLAB GUI设计一个控制面板，通过控制面板可以随时改变锁相环的环路参数，也可以接收锁相环通过USB传输给电脑的锁相环的结果。

三、设计原理

随着数字技术的发展，现在出现了很多资源丰富的可编程器件，像FPGA、DSP、专用集成电路等，基于软件无线电的通信系统，一般采用数字锁相环。数字锁相环具有锁定精度高，跟踪带宽大，参数可以在不修改硬件电路的前提下进行修改等种种的优点。目前，数字锁相环广泛应用于通信、航天等领域。针对具体的应用，数字锁相环可以用于载波跟踪，相位提取等。本设计就是以载波回复环为依托进行的数字锁相环设计。

(1)、锁相环的基本框架

锁相环是一个频率与相位的同步控制系统。它的工作过程可用下图表示

上面的锁相环是一般模拟锁相环所必需包含的环路组成，包括鉴相器、环路滤波器、压控振荡器。而对于利用软件来实现的全数字锁相环，必须在FPGA内部实现锁相环的鉴相器、环路滤波器、压控振荡器等部件。

(2)、本设计所要实现的锁相环的基本框架

本设计中，鉴相器有CORDIC混频器加上修正的arctan相位提取器组成，环路滤波器有理想二阶环组成，NCO由32位的数字累加器组成。

下面就比较重要的几个模块进行介绍

1、数字前端AGC模块

数字前端模块的框图如下：

数字前端模块接收来自ADC的采样数据，然后分成两路输出给载波恢复模块。输入到ADC的模拟信号频率为

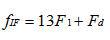
，ADC的采样频率为。这种IQ采样过程把ADC的输出数据频谱搬移到附近。在数字前端模块中，把输入的数据分成I、Q两路，然后数字混频到基带。这个数字混频只是简单的乘上频率为

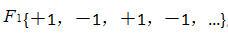
序列，不会产生二次频，因此后续不需要滤波处理。信号处理过程的数学表达式如下，假定ADC的中频输入信号为一简单的正弦波：

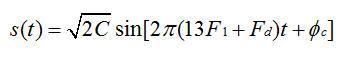
ADC的输出为：

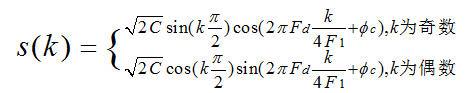
经奇偶分离和数字混频后，输出的I、Q两路信号分别为：

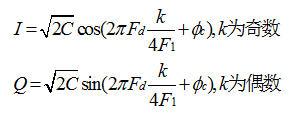
这两路信号在频域上存在2F1频率附近的频谱，因此必须把这个频谱消除掉。本设计采用了直接抽去掉0的方法，抽取后I，Q两路信号的数据速率从4F1降到了2F1。

经抽取后的两路信号分别为：

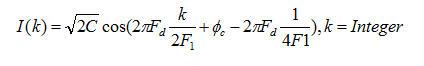
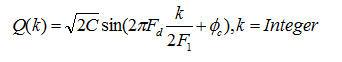
从上两式可见，直接抽取的方法会使I、Q两路信号之间存在一个跟采样频率及多普勒频偏有关的固定相位偏差

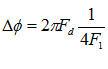
但是由于

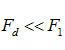
因此这个偏差非常小，在本设计中就不考虑这个固定偏差了。于是

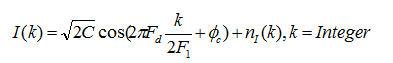
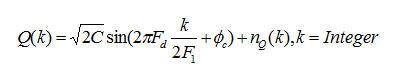
其中和都为零均值的高斯噪声，且互不相关，方差为，其中是单边带噪声功率谱密度。

一般载波跟踪环要工作在很大的动态范围下，为了使环路带宽和阻尼系数变化范围不要太大，从而使环路处于正常的工作状态下，必须控制环路内的信号强度，因为环路带宽和阻尼系数与信号强度有关。

AGC使信号可以保持一个近乎恒定的信号强度，增大了环路的动态范围，影响的是信号的功率或幅度，而对于相位几乎没有影响。AGC是采用了相干AGC的处理方法，由于它对于相位无影响，它的作用只是输出一个幅度尽量恒定的信号，因此这里就不讨论AGC的算法了。2、CORDIC 混频器

CORDIC是一种迭代的算术计算算法，通过相位旋转的方式能求各种基本函数的值。基于移位-相加方式实现的CORDIC算法是一种高效的硬件处理算法，非常适合在FPGA中应用。直角坐标系中，旋转矢量[x, y]和相位 的关系图如下：

其方程如下：

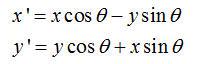
上式可改写为：

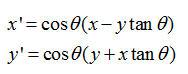
如果把旋转的角度限定为

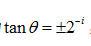
，即

，

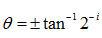
上式中与正切相乘的算法就简化为移位操作，因此迭代的旋转算法可以