基于神经网络的微波均衡器建模与仿真

其中J是包含网络误差对权值及阈值的一阶导数的雅可比矩阵。

牛顿法能够更快更准确地逼近一个最小误差，在每一步成功后，μ都会减小，只有当发现下一步输出变坏时才增加μ。按这种方法，算法的每一步运行都会使目标函数向好的方向发展。
　　算法开始时，μ取小值μ=0.001。如果某一步不能减小E，则将μ乘以10后再重复这步，最后使E下降。如果某一步产生了更小的E，则将μ乘以0.1继续运行。算法的执行步骤如图3所示。

对于RBF网络与BP网络的主要区别在于使用不同的作用函数，BP网络中的隐层节点使用的是Sigmoid函数，其函数值在输入空间中无限大的范围内为非零值。而RBF网络的作用函数为高斯函数，因而其对任意的输入均有高斯函数值大于零的特性，从而失去调整权值的优点。但加入LM算法进行网络训练后，RBF网络也同样具备局部逼近网络学习收敛快的优点，可在一定程度上克服高斯函数不具备紧密性的缺点。由于RBF网络采用高斯函数，表示形式简单，即使对于多变量输入也不增加太多的复杂性。
2.3 仿真设计结果
　　在建模过程中，如果要建立精确的神经网络模型，通常需要提供大量的训练样本。而在课题开展过程中，针对微波均衡器的复杂特性提出了以海量数据库为基础的网络子结构互联分析方法。这一方法的提出为建立均衡器神经网络模型提供了大量准确的训练样本。
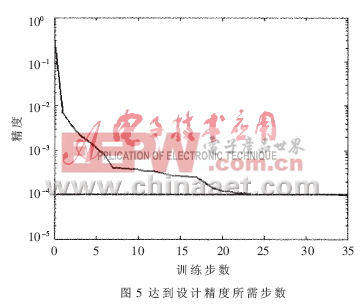
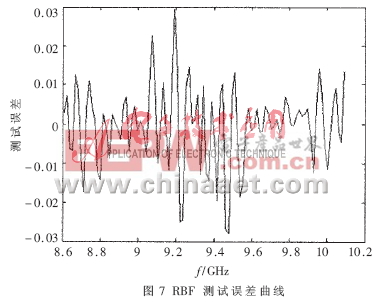
　　文中采用加入LM算法进行网络训练的RBF网络对均衡器进行建模，将均衡器的结构尺寸（谐振腔的腔长、探针插入主传输线的深度、吸收材料插入深度）和频率作为神经网络的输入样本，S参数作为输出样本，进行RBF网络训练。总共选取了100组样点作为训练数据，另外又选取了100组不同的样点作为神经网络模型性能的测试数据。频率8.6GHz≤freq≤10.092 5GHz。模拟S参数与输入样本间的关系：Y=F(X)，其中：X是神经网络的输入变量；Y是输出变量，Y=(|S11|,|S21|)。利用MATLAB软件仿真输出变量中|S21|的仿真和训练结果如图4～图7所示。其中，图4为RBF网络的仿真曲线, 由此可见误差非常小。图5给出了达到预期的设计精度0.000 1所需的训练步数为35步，此网络很快即达到了设计精度。为了验证训练后的RBF网络的性能，另选取100组样点进行测试，其测试曲线如图6所示，RBF网络的测试性能可由图7所示，测试绝对误差的绝对值小于0.03，98%的测试相对误差小于5%，在|S21|衰减最大的拐点位置相对误差较大，这是因为测试样点在拐点处的选取没能满足实验设计（DOE）原则。仿真输出再次说明RBF神经网络建模的性能相当稳定。而且利用该神经网络进行仿真设计的结果具有很好的可重复性，设计达到的效果令人满意。

本文采用RBF神经网络对微波均衡器进行了建模。仿真设计的结果与网络分析仪的测试结果进行了比较，误差较小。这表明本文提出的神经网络模型设计方法使得微波均衡器的设计过程变得速度快、精度高，具有准确、省时、辅助设计等优点。对于微波器件的分析设计具有很好的应用价值。