基于神经网络的微波均衡器建模与仿真
大功率行波管等微波管是雷达等电子装备的核心器件,其技术水平决定了电子装备的战术性能。但是由于大功率微波管的增益波动较大,在等激励输入的情况下,不能使频带内所有点均达到饱和输出,这样会造成输入信号产生谐波和互调分量,导致微波真空管次品率上升,更重要的是直接影响了现代电子设备的性能,特别是难以满足现代战争的高环境可靠性要求。因此,需要使用大功率微波管均衡技术,即增加一个微波网络,使其传输特性与微波管的传输特性相补偿,这样行波管的输出功率波动减至最小,该微波网络就是微波均衡器。
而多谐振腔结构的均衡器是具有复杂微波结构的器件,由于其结构的复杂性使得其严格数学表示非常复杂,无论用解析方法还是数值方法,直接的求解都很难进行,而对各种非理想因素进行简化后的计算结果误差又太大,实用价值不高。在无法得到其准确电磁特性的条件下,无法对调试工作进行有效的指导,优化设计更无从谈起。这一问题对于目前微波工程中普遍应用的复杂微波结构来讲,也是普遍存在的,而且也是一个急需解决的问题,因此为了提高设计速度,节省设计成本,对均衡器建立模型,用于计算机辅助设计显得越来越重要。
微波均衡器的传输特性主要决定于它本身的结构尺寸和频率,它们构成非线性映射关系,而神经网络可以对任何线性和非线性的函数关系进行快速、准确的模拟,并且具有良好的联想能力。故可以采用人工神经网络对均衡器进行建模。虽然神经网络的训练过程需要花费一定的时间,但是神经网络模型一旦训练完成,就可以在很短的时间内得出结果,且不会牺牲精度,因此采用神经网络模型辅助微波均衡器的设计将会大大提高设计速度,节省调试时间。
1 均衡器基本单腔子结构
图1是吸收型同轴微波幅度均衡器的单子结构图,多子结构级联的情况以此为基础。同轴谐振腔的一端与主传输线相连,另一端是可调短路活塞,它可调节谐振腔腔长,谐振腔内是插入主传输线的可调耦合探针,通过探针将主传输线内的能量耦合入谐振腔,改变谐振腔腔长和探针插入深度可调节谐振腔的谐振频率和品质因数Q值等。另外,还可以在谐振腔侧壁的适当位置插入吸收材料制成的衰减棒等。
但由于单子结构带宽和吸收衰减幅度的有限性,为了能在较宽频带内实现对大功率微波管的高精度均衡,必须采用多级子结构级联的形式。所以在工程实践中,针对均衡器的复杂特性提出了以海量数据库为基础的网络子结构互联分析方法。在数据库的建立过程中,利用网络分析仪对均衡器单腔子结构进行S参数的测量,建立相应的S参数测量数据库。此数据库中每个测量点对应的均衡器物理参数为:谐振腔的腔长Lc,耦合探针插入传输线深度Ls,介质微扰插入谐振腔深度La。由工程实践可知,三个物理参数对谐振频率点的频率影响是有规律可循的。通常,谐振频率随Lc的增大而降低;谐振频率随Ls的增大而降低,同时衰减增大;谐振频率随La的增大而降低,同时衰减减小。
2 神经网络模型设计
2.1 RBF神经网络
RBF(Radius Base Function)是最近十年兴起的一种新型的神经网络,它具有网络结构简单、网络训练速度快(与BP算法相比,RBF网络的训练算法可以快一个数量级)、仿真精度高等优点。RBF网络同时具有良好的局部性,能提供平滑、性能优秀的离散数据内插特性,由该网络构成的系统是有界、稳定的。
RBF神经网络的结构如图2所示,它是一种两层网络,第一层由RBF神经元作为隐神经元(传输函数为高斯函数),图中a1i的表示向量a1的第i个元素;b1i表示向量b1的第i个元素(即第i个RBF神经元的方差);iW1表示矩阵W1的第i行,即第i个神经元的中心。第二层由线性神经元(传输函数为线性函数)作为输出神经元。其中S1、S2分别表示第一层和第二层神经元的数目。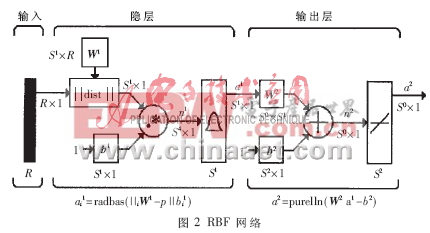
若考虑S2=1的情况,此时把整个神经网络看成一个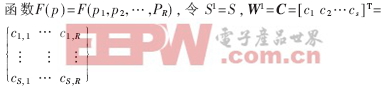
其中,ci(i=1,2,…,S)为矩阵C的每一行,它代表相应神经元径向基函数的中心向量,b1=λ=(λ1,λ2,…λS),其中λi代表径向基函数的方差,W2=W=(w1,w2,…,wS),则网路输出为:
2.2 网络的训练
仅仅搭建这样一个模型是没有意义的,神经网络在实际工作之前必须进行学习,通过学习,神经网络才能获得一定的“智能”。
学习是神经网络一种最重要也最令人瞩目的特点。在神经网络的发展进程中,学习算法的研究有着十分重要的地位。目前,人们所提出的神经网络模型都是与学习算法相对应的。所以,有时人们并不苛求对模型和算法进行严格的定义或区分。有的模型可以有多种算法,而有的算法可能用于多种模型。
本文根据均衡器的传输特性,在训练学习过程中,其连接权值的不断调整以及学习修正采用BP网络学习算法中的LM算法。LM算法是为了训练中等规模的前馈神经网络而提出的最快速算法,它对MATLAB实现也是相当有效的,在BP网络的众多学习算法中,通常对于包含数百个权值的函数逼近网络,LM算法的收敛速度最快。如果要求的精度比较高,则该算法的优点尤其突出。在许多情况下,采用LM算法的训练函数trainlm可以获得比其他算法更小的均方误差。
LM算法实际上是梯度下降法和牛顿法的结合。梯度下降法在开始的几步下降较快,当接近最优值时,由于梯度趋于零,使得目标函数下降缓慢;而牛顿法可以在最优值附近产生一个理想的搜索方向。其主要算法为: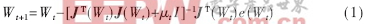
建模 仿真 均衡器 微波 神经网络 基于 微波均衡器 人工神经网络 RBF网络 相关文章:
- 新型建模算法简化天线设计(04-29)
- 基于IEC61850标准的ACSI服务模型研究(12-20)
- 基于IEC61850标准中SCL的智能电子设备建模(10-22)
- 双软扩频与π/4DPSK复合调制系统建模仿真(02-21)
- 贝叶斯网络在学生模型建模中的应用分析(06-17)
- 基于C3I系统的短波通信仿真建模(09-23)
