cdma2000-1x系统中GPS时钟算法

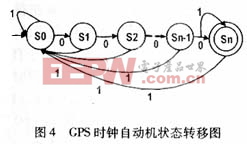
在状态S0、S1、S2.......Sn的迁移过程中，在不同状态下分别完成打开GPS时钟、读取GPS时钟、计算GPS时钟、关闭GPS时钟等一系列动作。在状态Sn处，我们已通过串口获得GPS软件时钟，且此软件时钟中20ms中断维护计数器加1（此GPS时钟的精度单位为20ms），保证时钟正常运行；在某个循环周期内通过2S中断重新获取时钟，并对时钟精度进行校正。在正确得到GPS时钟后，通常情况下，时钟处于稳定状态，此时GPS时钟自动机在状态Sn处循环运行。
　　当时钟自动机条件转移参数值为1时，此状况通常由以下情况造成：
　　情况一：GPS时钟模块在信号的解析过程中丢失了一个1.25 ms中断；
　　情况二：GPS时钟模块在信号的解析过程中丢失了一个2S中断；
　　情况三：其他原因（如多了一个1.25ms中断或多了一个2S中断等情况）。
　　若状态转移参数值为1，自动机状态将迁移到初始状态S0，并重新获取并校正GPS时钟。每经过一个2S中断，时钟状态将根据条件转移参数值的不同进行状态间的迁移，重新取时钟并进行时钟校正。若GPS时钟的2S中断和20ms中断连续稳定，自动机将处于稳定态Sn，并且由20ms中断继续维护当前的软件时钟，为上层提供持续不断的时钟，时钟校正后更新当前时钟。
　　此自动机具有如下性质：
　　安全性：本文提出的GPS时钟自动机不含任何等待不可能发生事件的状态，即自动机无死锁；收到预期条件转移会跳出等待循环，即自动机无活锁；
　　完整性：自动机不含未定义的条件转移参数，包括正常和异常处理，即自动机具有完整性；
　　活动性：经过有限步可回到初态，且无不可达态，即自动机具有活动性。

三、GPS时钟算法分析
　　根据本算法所取得的GPS软件时钟与标准时之间的时钟误差精度主要是由于1.25ms中断与2S中断的不稳定性决定。
1.时钟精度分析
　　由20ms中断和1.25ms中断时序（图2）可以看出，在20ms中断中出现的1.25ms中断的个数一定是16个（由硬件实现），但由于1.25ms中断可能丢失或增加等情况，这就造成了两个相邻20ms中断间隔并非完全是20ms，这将改变GPS时钟自动机的条件转移参数值为1；若丢失或增加一个2S中断，也会改变GPS时钟自动机的条件转移参数值为1。以上两种情况就增加了所维护的GPS时钟的不稳定性因素。我们定义标准时间为T,算法所取到的时间为T′，2S中断处理时间为Δ。下面将讨论它们的具体关系（对条件转移参数值为1时的3种情况进行讨论）：
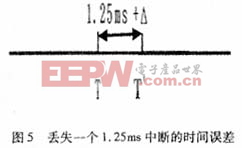
　　情况一：这种情况发生的概率相对来说较大。若丢失一个1.25ms中断，由于20ms中断之间必须保证有16个1.25ms中断，也就是说即将到来的20ms中断比标准时将推迟1.25ms+Δ，见图5。

情况二：这种情况发生的概率相对来说较小。丢失一个2S中断，将会使条件转移参数值为1，使自动机当前状态迁移到初始状态，自动机将重新获取时钟并校正时钟，但不会影响时钟精度。
　　情况三：这种情况发生的概率微乎其微。但若1.25ms中断多了一个，也就是说即将到来的20ms中断比标准时将提前1.25ms-Δ（见图6）；若多了一个2S中断，自动机将重新获取并校正时钟，但不会影响时钟的精度。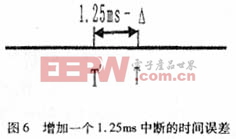

我们对连续的1.25ms中断进行分析，假设每次1.25ms中断正确到来的概率为p，丢失或增加了一个1.25ms中断的概率为q（稳定情况下每天平均±1×10-11,失锁保持稳定情况下每天平均(1×10-10），其中p+q=1。对以上3种情况，我们进行k次取样，假设前k-1次1.25ms中断均正确到达，但第k次1.25 ms中断丢失或增加了一个1.25ms中断的概率为p{X=k}，此随机变量X符合几何分布［5］，即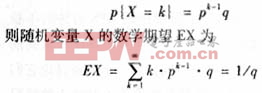

也就是说，平均有1/(1-p)个1.25ms中断中将有一个1.25ms中断丢失或增加。
　　令从GPS时钟自动机的初态开始运行到现在的总时间为Tw，每两个相邻的1.25ms中断时间为T0=1.25ms，假设GPS时钟的误差精度为ΔT,本算法计算的GPS时钟时间为T′，标准时间为T,所以时钟误差［3，4，5］为

2.参数选取分析
　　对本文的GPS时钟自动机状态数n进行讨论。我们以MPC 860处理器为例，一个时钟周期大约为20 ns。计算GPS时钟时间可能要有以下步骤：
　　(1)清空2S中断中20ms中断个数计数器，设置初始状态S0，重新定位标准输入/输出，使与串口脱离，从而避免标准输入将输入的东西截走，此操作一般需60 ns左右；
　　(2)打开GPS时钟，设置串口信息，此操作一般需30 ns左右。设串口速率为9 600 bit/s，从串口读时钟送到缓冲区大约需50 ms；
　　(3)从缓冲区读GPS时钟，计算并设置当前时间，此操作一般需1μs左右；
　　(4)校正GPS时钟，关闭GPS时钟，并将标准输入/输出重新定向，此操作一般需60 ns左右。
　　以上任意两个步骤是不能并行完成的，因此我们取GPS时钟自动机状态数n为4。由于自动机在终态S4的开销时间为60 ns（即中断处理时间Δ），此时我们的时钟误差重新校正为ΔT ∈(-1.25 ms×m+60 ns,1.25 ms×m+20 ns+10 ns+60 ns)，即ΔT ∈ (-1.25 ms×m+60 ns, 1.25 ms×m+90 ns)。
　　通常情况下q的理论值在±1×10-10，此时随机变量X的数学期望值EX为1/±1×10-10 =±1×1010。但在GPS设备的使用过程中时钟精度会随设备的老化或其他因素而进行漂移，这是我们必须要考虑的因素。我们假设最坏情况下值q∈ (±1×10-11,±1×10-8)范围内，总时间为Tw（Tw与q之间确定的参数m值见表1）,则时间t（单位为天）与时钟误差ΔT的关系如图7。