基奇PCA的贝叶斯网络分粪器研究

1 引言
近几年来，贝叶斯网络已成为数据挖掘和知识发现中的一个主要工具，在分类、聚类、预测和规则推导等方面取得了良好的应用效果。从历史数据中学习贝叶斯网络可采用基于依赖分析的方法。
常用的有：用Polytree表示概率网的方法、从完全图删除边的方法等。这种方法需要进行指数级的CI测试以发现依赖关系，当结点集较大时，其计算效率低，所以大多数此类算法都假设结点有序；但这种假设可能会影响最后学习到的网络结构的正确性。对于稀疏网络和具有较大样本数据集的系统，这种方法非常有效。
针对基于依赖分析方法的这一缺点，在网络结构学习之前应用主元分析方法将数据降维，减少网络结点数目，可提高算法效率、简化网络结构。

2 数据处理及离散化
现实数据库中的数据常存在数据不一致、数据丢失等现象，所以在运用数据学习网络结构前要对数据进行预处理。此外，对于连续性数据(如温度、湿度、长度等)，直接建立贝叶斯网络模型计算复杂度大，从连续数据中很难正确学习到变量间的关系。因此首先将数据标准化，再将标准化后的连续变量离散化，用离散化后的数据进行贝叶斯网络结构的学习。这里采用模糊离散化方法，对数据集的每个属性分别进行离散化，每个属性都有3个标度：5标度、7标度、9标度可以选择。算法步骤如下：
(1)随机初始化隶属度矩阵：

3 基于PCA的贝叶斯网络结构学习算法
主元分析PCA(Principal Component Analysis)是通过可逆线性变换，将数据集转换为由维数较少的特征成分表示的、包含原数据集所有信息或大部分信息的技术。通过PCA技术，可以将复杂数据简化，因此它现已被广泛应用于数据挖掘、模式识别、信号评估、信号探测、图像编码等领域。主元分析的原理如下：
令x为表示环境的m维随机向量。假设x均值为零，即

E[x]=0 (4)
令w表示m维单位向量，x在ω上投影。该投影被定义为向量x和ω的内积，表示为：

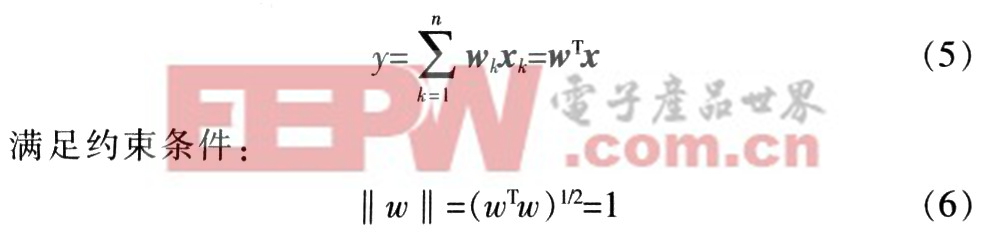
主元分析的目的就是寻找一个权值向量w，使得表达式的值最大化：

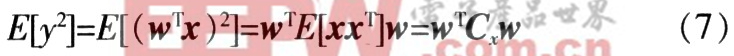
即使得式(7)值最大化的w是矩阵的最大特征值所对应的特征向量。
鉴于主元分析的优点，这里引入主元分析技术给数据集降维，然后用降维后的数据构建网络，提高学习贝叶斯网络结构算法的效率、简化网络结构。构造贝叶斯网络的算法步骤如下：
(1)用普瑞姆算法生成最大似然树构造初始贝叶斯网络；
(2)对所有互信息大于阈值且在当前图中无边的结点对n1、n2：①找出它们邻接路径上的邻居结点，设n1、n2的邻居结点的结点集分别为S1和S2；② 令集合S1和S2中较小的一个作为条件集合C；③计算条件互信息v=I(n1，n2|c)，如果vε，则返回分离；否则，如果C只包含一个结点，那么转去步骤⑤，否则，对每一个i，令Ci=c{C中的第i个结点}，vi=I(n1，n2|Ci)；④如果vminε，则返回分离，否则返回步骤③；⑤如果S2没有用过，那么用S2作为条件集C，返回步骤③；否则，返回失败。⑥如果这对结点在当前图中能够被分离，则检测下一对结点，否则，向网中添加连接这对结点的边。
(3)对每一条图中存在边的结点对，如果除这条边外它们之间还存在其他路径，那么暂时从图中移掉这条边，然后对这对结点进行步骤①～⑥的检验；如果这对结点不能被分离，则仍将前面移掉的边加入图中，否则永久移除这条边；
(4)用碰撞识别V结构的方法定向网络中的边，对不能构成V结构的边用打分的方法对其进行定向。

4 实验
用IRIS实际数据、Zoo Data、Glass Identification Data作为网络学习的数据集，这3组数据是UCI数据集中3个用于分类的数据集。
其中IRIS数据和Glass Identification Data是连续的，所以在用数据学习贝叶斯网络前需要对数据进行模糊离散化处理。以下实验中的每个属性的离散化标度是任意选择的。实验1，比较经PCA降维的数据构造贝叶斯网络并进行分类的结果与未经PCA降维的数据分类结果的准确率，如表1所示。

用经PCA降维的数据和未经降维的数据集分别进行贝叶斯网络结构的学习，所用时间如表2所示。

对所用的贝叶斯网络学习算法进行CI测试，最坏情况下的时间复杂度为O(N4)。由表2可知，采用PCA降维后，算法所用时间约占原构造算法时间的34．58％，贝叶斯网络结构的学习效率有所提高。
经PCA降维，IRIS数据集的属性由4个减少为3个；ZooData的属性由18个减少到12个；Glass Identification Data的属性由11个减少为8个。属性数量的减少使得网络结构更为简单，并且由表2可以看出，经PCA降维后进行分类的结果准确率不低于不经过降维直接由数据集学习得到的贝叶斯网络分类结果的准确率。
经PCA降维后的网络结构如图1～图3所示。

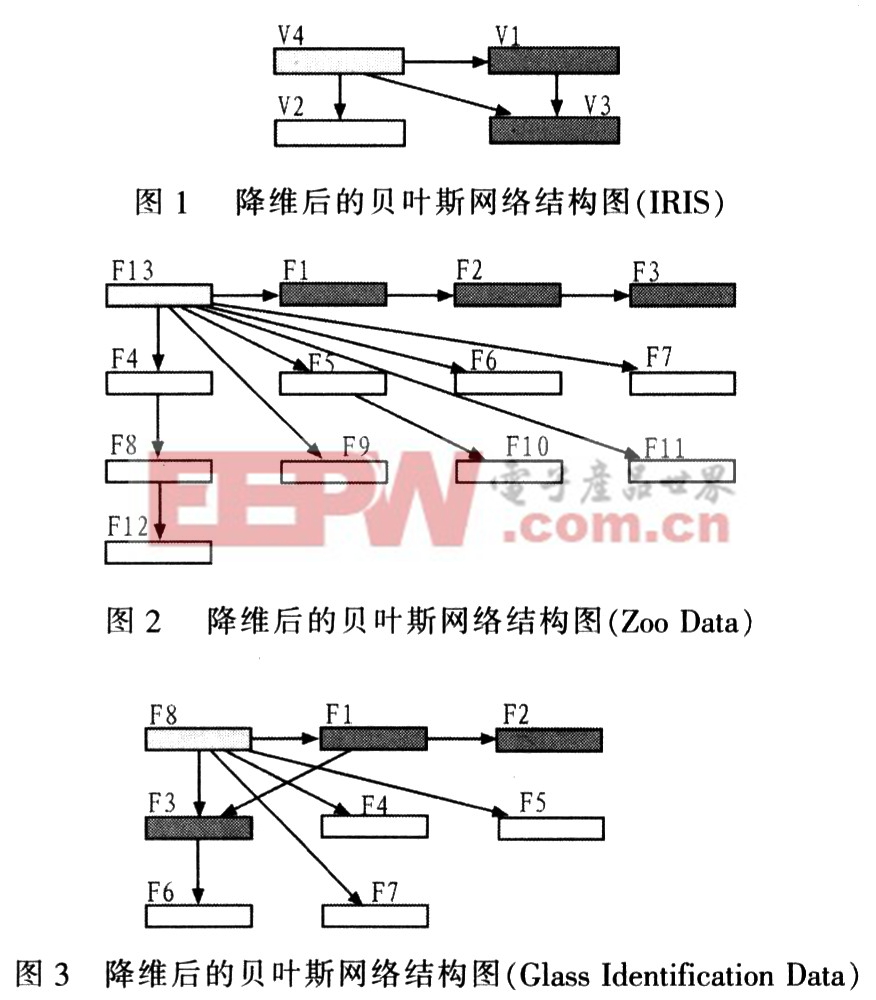
用图1中的结