BTS 系统中开环和闭环 MIMO 的应用

空间复用

空间复用是一种非常著名的开环MIMO技术，广泛应用于无线系统。每个发射天线送出不同的数据流。

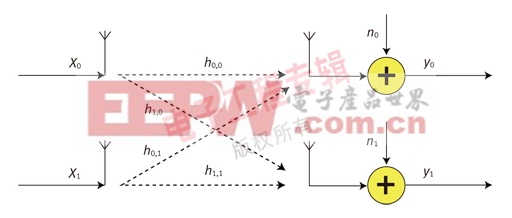
图1：2x2 空间复用系统。

图1是一个2x2的空间复用系统，可以建模为：

(1)

其中x代表发射信号向量，H代表信道矩阵，n代表增加的噪声向量，y代表接收信号向量。为了根据接收信号y评估发射信号x，直接的方法就是用迫零(zero forcing)或MMSE等逆信道矩阵乘以y。然而，这并非最佳检测方法。

最理想的检测方法可利用最大似然法(ML)准则。在大多数情况下，发射信号向量最大限度缩短了与接收信号向量y相关的欧几里得距离，因此，可以通过寻找发射信号向量来执行最大似然法。

(2)

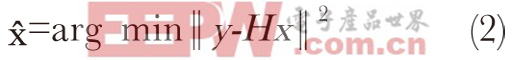
可惜，计算的复杂性也随着发射天线和可能的星座点的数量呈指数增加，这使最大似然法无法适于实际用途。

球形解码(sphere decoding)虽然不是最理想的ML解决方案，却是一种广泛使用的方法。球形解码算法的原理，是在球半径内搜索离接收信号最近的格点。在球半径内，格点场的每个格点都代表一个码字。球形解码显著降低了检测的复杂性，其性能可与ML检测方法相匹敌。

然而，尽管球形解码算法已经降低了复杂性，却不适于实施大量天线和64QAM等高调制率。

空时码

另一个广泛采用的开环MIMO是空时码。利用空时码，一个数据流可以用多个发射天线传输，但是信号编码利用多个天线中的独立衰落，以实现空间分集。

图2：典型的Alamouti码。

目前，最受欢迎的空时码是Alamouti码，已被许多无线标准采用。图2为典型Alamouti码，其数学方程式表述如下：

(3)

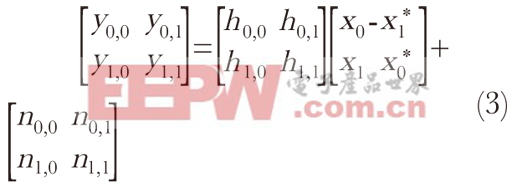
通过重新整理方程，可以得到：

(4)

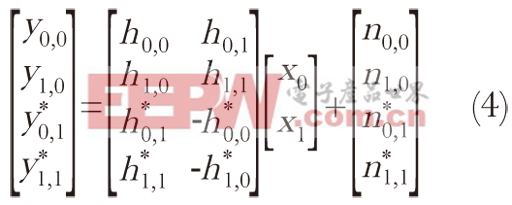
方程(4)显示，信号x₀和x₁在两个直角路径中传输。因此，只需简单的线性处理，就可以单独检测和 。

与空间复用相比，Alamouti码可提供更高的分集增益，且不需要复杂的接收机检测。然而，Alamouti码只传输一个数据流而非多个数据流。空间复用着眼于空间复用增益，但是空时码则瞄准分集增益。要比较这两个方案，我要应该考虑信道条件。一种方案只有在特定信道条件下才会优于另一种技术。许多无线标准采用了这两个方案。如何在两个方案间进行转换以实现最佳性能呢？R.W.Heath Jr. 和A.J. Paulraj 在《MIMO系统中分集和复用的转换》[1]一文中提出了如何选择分集增益或复用增益的标准，即选择能缩短接收机欧氏距离的方案。然而，这种方法需要繁复的搜索，因此不适合实施。为了解决这个问题，本文建议使用Demmel 条件数进行选择。事实上，这是非常直观的。对于大Demmel条件数，信道更有可能是奇异的，因此应选择空时码。

在现代无线通信领域，闭环MIMO变得越来越重要。BTS发射机利用信道信息实现简单空间分集或波束成形技术，以提高系统的有效SNR，并可能简化Rx架构。

我们用两个Tx天线和两个Rx天线举例说明闭环MIMO。如果 Tx具有H信道的完整信息，最理想的传输方案为：

(5)

其中x是2x1发射信号向量；s是2x1信息向量；W是注水矩阵。

(6)

若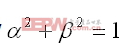，V就是H的SVD中右边的酉矩阵。

通过酉矩阵V，H信道被分成两个直角路径。利用注水矩阵，用更高的SNR为数据流分配更多功率，我们能够获得最大的容量。应该注意的是，如果我们设置，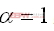

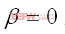，这表示我们将全部功率用于具有更高SNR的路径，只传输单信号流，这便成为最好的SNR解决方案。

这里主要的问题是如何获得发射机的信道信息。最新的无