一种新型加载Sierpinski垫片天线的设计

摘要：提出一种新型分形结构加载的Sierpinski垫片天线。该天线采用新型加载技术并充分利用了此新型结构的空间自填充能力。结果表明，此新型分形结构加载的Sierpinski垫片天线比Koch分形加载更能缩减天线的尺寸，并且能降低谐振频率，具有宽频带特性，可以实现 Sierpinski分形天线的小型化、多频段特性。
关键词：Sierpinski垫片天线；RFID；宽频带；小型化

0 引言
射频识别(Radio Frequency Identification，RFID)是20世纪90年代兴起的一项自动识别技术。该技术利用无接触方式获取目标信息，并与目标信息进行双向通信。由于其无接触的工作特性，它被称为第三代自动识别技术。一个自动识别系统有两个部分组成：读写器和电子标签。天线在读写器和电子标签中间担当着十分重要的作用，它是两者之间实现非接触双向通信必不可少的器件。天线被用来发射和接收信号，并且担当着电子标签芯片中耦合能量的重要作用。所以电子标签天线设计的好坏直接影响着系统的工作距离以及使用范围。
在RFID系统应用中，电子标签天线需要附着在需要识别的物体上，作为识别物品的身份象征，并且由于被识别物体的多样性，人们对电子标签天线提出了更高的要求，主要体现在宽频带、小型化、便于安装和携带，同时要求天线有高的效率。天线设计很大程度依赖天线的频率，有些类型的天线具有很宽的带宽，如螺旋天线。这种天线从某种意义上来说是分形天线的自相似性具体化，分形天线的自相似性对于电子标签天线的设计具有具有重要意义。
分形天线是一种新型天线，它将分形几何应用于天线，完全不同于传统意义上的欧式几何天线。分形结构的高度空间自填充特性可以转变为分形天线的小型化特征，例如Koch分形天线、Hilbert分形天线、Minkinski分形天线等。分形结构的自相似性可以转变为分形天线的多频段特性，典型的有 Sierpinski分形天线。
本文提出了一种新型分形天线加载的Sierpinski垫片天线，与传统天线相比，此天线充分利用了新型分形结构的高度自填充性以及Sierpinski分形天线的的多频段特性，从而实现了一种新型的小型化、多频段分形天线。

1 分形结构的几何描述和天线生成
分形结构的天线构造形式很多，本文采用两点格式法进行构造新型分形天线。先定义一个初始元和一个生成元，初始元给定了分形图形的框架，生成元给定了新型分形天线的构造方法。此新型分形天线的初始元和生成元如图1所示。


图1中符号的上标代表迭代次数，下标代表坐标点。选取：

式中：k=1／4为分形凹入的宽度。
由分形理论可以知道，该新型分型结构的分形维数D取决于以下方程：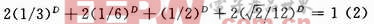

通过1阶生成元的迭代过程，可以进行再次迭代得到2阶及3阶生成元。虽然此新型分形曲线具有与Koch分形结构相同的迭代特性以及空间填充特性，但是分形迭代在实际中不可能无限制的迭代下去，研究发现，此新型曲线在降低谐振频率上有一个极限值，一般在5阶以上性能就不明显了，这里称之为分形极限。同时，由于现代制造工艺的限制，一般分型天线都在5阶以下。
此新型分形曲线同Koch分形曲线有很多相似之处，1阶新型分形曲线比1阶Koch曲线长30．18％，2阶新型分形曲线比同阶的Koch曲线长1．44 倍，而且具有分形天线的特性。由此可以说明，此分形天线具有比Koch分形结构更强的自填充能力，用在天线设计中可以实现更长的电流有效路径，从而降低谐振频率，实现天线的小型化。

2 Sierpinski分形天线
Sierpinski三角形是由波兰数学家Sierpinski提出的一种分形结构，图2显示了使用迭代函数系统(IFS)构造Sierpinski分形天线的过程，它的分形维数为：D=In 3／In 2=1．58。


2．1 Sierpinski分形结构的边长对天线性能的影响
对于Sierpinski分形天线，这里研究了角度均为600，比例因子均为0．5时，三角形的边长分别为48 mm，56 mm，60 mm时，基于0阶和1阶的偶极子天线性能。天线结构如图3所示。利用HFSS 11．0进行仿真，其中1阶分形结构仅列出低频谐振频率，仿真结果如表1所示。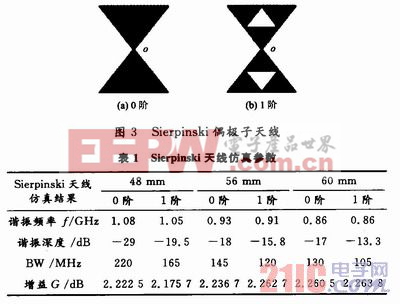


表1仿真结果表明：在天线比例因子不变，角度不变的条件下，随着边长的增长，谐振频率、谐振深度、带宽BW(VSWR2)均在逐渐减小，这是由于增益虽然变化不是十分明显，但是依然可以看出边长为60 mm时天线的增益最大，这有益于天线校正。总之，基于Sierpinski分形结构的天线的第一谐振频率与天线的周长和高度有关。在保持天线的周长和高度不变的条件下，阶数的变化不会影响第一谐振频率点。
2．2 角度不同，对天线性能的影响
对于0阶Sierpinski分形天线而言，其实它就是两块三角形的平板，三角形板型天线为宽频带天线，这里研究当其两条边相同，但其所夹角不同时，天线的性能。天线的边长为60 mm时，所夹角分别为30°，60°，90°，由HFSS 11．O仿真得其天线性能如表2所示。


从表2的仿真结果可以看出，角度为30°时，其天线的增益最大，同时，无论是角度大小，其谐振频率基本上是不变的。这是因为，对于Sierpinski垫片分天线而言，电流主要沿着三角形的两条边流动，而此时天线的边长都相等，所以谐振频率基本不变。
2．3 比例因子对天线性能的影响
文献中比较了张角θ=60°不变的条件下，比例因子δ分别为1．5和1．67对Sierpinski分形天线谐振频率的影响。结果表明随着比列因子δ的减小，天线的谐振频率将向低频端移动。每种天线相邻谐振频率间的比率除第一个以外，均与其各自的比例因子值基本相同。谐振频率间的第一个比值相对偏大，这是因为在天线的低频段，电流分布于整个天线表面，天线的终端效应比较强的缘故。研究表明Sierpinski分形天线迭代次数的增加，会出现多个谐振频率点，且第一个谐振频率点与三角形的高度有关，辐射方向图与天线在空间的分布有关，而与天线的迭代次数没有关系。同时也给出，当角度减小到一定程度时，天线的多频段特性均不明显。

3 新型分形加载的Sierpinski垫片天线
基于以上分析，设计出一款谐振在915 MHz新型加载Sierpinski垫片偶极子天线，此天线采用NXPG2XM标签芯片，其参数为在915 MHz时，芯片对外呈现阻抗为22-j195 Ω，天线的大小为96 mm×54 mm，它由顶角为60°的1阶Sierpinski分形和顶角为30°的0阶Sierpinski分形组成，在1阶Sierpinski分形天线的两边加载新型分形天线，中间点为馈电点。天线模型如图4所示。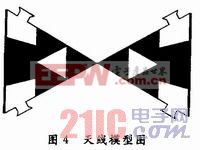


此天线利用新型分形加载Sierpinski天线，由于Sierpinski天线的电流主要沿着三角形的两条边流动，在三角形的两条边上加载新型分形天线，有效延长了电流的有效路径，进而可以降低天线的谐振频率。同时，新型加载从另一个角度来说，在角度不变的条件下，使三角形的高度增加，有效延展天线电流有效路径，减小了天线的大小。利用夹角为30°的0阶Sierpinski垫片天线高增益、宽频带特性，在谐振频段内实现了比较深的谐振深度，使得驻波比更小。通过HFSS 11．O仿真，天线的增益方向图如图5所示，图6为回波损耗曲线及驻波比曲线。