有源滤波器中的相位关系考察

在使用滤波器的应用中，通常人们对幅值响应的兴趣要比对相位响应的兴趣更浓厚。但是，在某些应用中，滤波器的相位响应也很重要。一个实例是 滤波器用于过程控制环路中的情形。这里，人们关心的是总的相移量，因为它影响到环路的稳定性。用来搭建滤波器的拓扑结构是否会造成在某些频率点处符号出现 相反，是非常重要的。

将有源滤波器视为两个级联的滤波器是一个有用的方法。如图1所示，其中一个滤波器是理想的滤波器，用于体现传递函 数;另一个是构成滤波器的放大器。在闭环的负反馈环路中所采用的放大器可以被视为一个具有一阶响应的、简单的低通滤波器。当频率超过某一点后，增益将随着 频率的增长而出现滚降现象。此外，如果放大器使用反相放大结构的话，则所有频率点上还将出现附加的180°相移。

图1. 以两个级联的传递函数的形式表示的滤波器

滤 波器设计过程可分为两步。首先选定滤波器的响应特性，接下来选出适当的电路结构来实现它。滤波器的响应是指衰减曲线的形状，这常常可以归为经典的响应特性 中的一种，如Butterworth、Bessel或者某种Chebyshev型。虽然这些响应特性的选择往往会影响幅值响应特性，但它们也会影响相位响 应特性的形状。在本文中，为了进行比较，忽略幅值响应，认为其几乎不变。

滤波器的复杂性往往通过滤波器的“阶数”来定义，该参数与储能元 件(电感和电容)的数量有关。滤波器传递函数分母的阶数定义了随着频率的上升而呈现的衰减速率。渐近线型的滤波器滚降速率为-6ndB/倍频程，或者 -20ndB/十倍频程，其中n是极点的数量。倍频程是指频率的二倍或者一半，十倍频程是频率的十倍增长或者缩减。因此，一个一阶(或者单极点)滤波器的 滚降速率为-6dB/倍频程或者-20dB/十倍频程。类似的，一个二阶(或者2极点)滤波器的滚降速率为-12dB/倍频程或者-40dB/十倍频程。 更高阶次的滤波器往往是由级联的一阶和二阶基本单元所构成的。自然，我们可以利用单个有源放大电路级来构建三阶、甚至四阶滤波器，但是对于元件值的敏感， 以及元件之间的相互作用对频率响应所造成影响的大幅度上升，会使这些选择不那么具有吸引力。

传递函数

首先，我们考察一下传递函数的相位响应。对于同样阶数的滤波器选项来说，它们的传递函数的相移特性都相同。

对于单极点、低通的情形，传递函数的相移为φ，由下式给出。

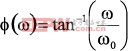
(1)

式中：ω = 频率(弧度/秒)

ω0 = 中心频率(弧度/秒)

以弧度/秒为单位的频率等于2π乘以以Hz为单位的频率，这是因为每个360°周期对应着2π弧度。由于上面的表达式是一个无量纲的比值，故f和ω都可以采用。

中 心频率还可以被称为截止频率(即该单极点、低通滤波器的幅值响应特性下降3dB——约30%——的频率点)。在相位关系方面，中心频率是相移量达到其最终 值-–90°(在这个例子中)的50%时的频率点。图2是一幅半对数图，描述了公式1所表述的相位响应关系，其频率范围是中心频率以下的两个十倍频程至中 心频率以上的两个十倍频程。中心频率(=1)处的相位移动为–45°。

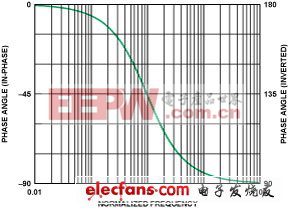
图2. 一个单极点、低通滤波器在中心频率附近的相位响应(同相，左轴;反相响应，右轴) 图中：Normalized Frequency——归一化频率，Phase Angle(in-phase)——相角(同相)，Phase Angle(inverted)——相角(反相)

类似的，一个单极点的高通滤波器可以由下式给出：

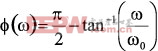
(2)

图3描绘了公式2所表示的、在中心频率以下两个十倍频程至中心频率以上两个十倍频程这一范围内的响应特性。其归一化的中心频率(=1)处的相移为+45°。

显然，高通和低通特性类似，只是相互间存在90°的相位差(π/2 radians)

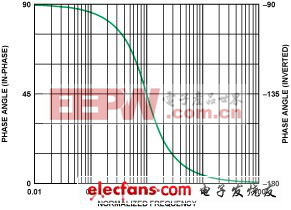
图3. 一个单极点、低通滤波器在中心频率 1 附近的相位响应(同相，左轴;反相响应，右轴) 图中：Normalized Frequency——归一化频率，Phase Angle(in-phase)——相角(同相)，Phase Angle(inverted)——相角(反相)

对于二阶、低通的情形，传递函数的相移可以由下式近似表示为

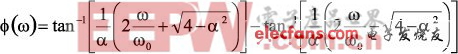
(3)

式 中α是滤波器的阻尼比。它将决定幅值响应曲线上的峰值以及相位曲线过渡段的陡峭程度。它是电路的Q值的倒数，这也决定了幅值滚降或相位偏移的陡峭程度。 Butterworth响应的α为1.414(Q=0.707)，可以产生最大平坦度响应特性。更低的α会使幅值响应特性曲线上出现尖峰。

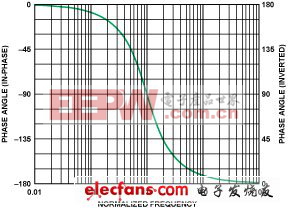
图4. 一个双极点、低通滤波器的中心频率 1 附近的相位响应(同相，左轴;反相响应，右轴) 图