∑-△模数转换器工作原理及简单分析

2.4 二阶噪声成型原理
图3显示二阶∑-△调制器结构原理。2次噪声整形电路是进行2次低频提升和低频衰减的电路,即在∑-△调制方式1 bit量化器的前后,分别加2级积分器和微分器构成的,如同1次噪声整形简化方式一样,2次噪声整形使噪声分布斜率更加陡峭,低频区量化噪声得到进一步降低。
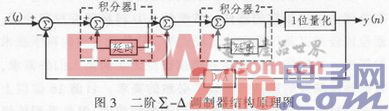
根据线性模型可推出二级∑-△调制器的方程为
y(kT)=x(kT-2T)+e(kT)-2e(kT-T)+e(kT-2T) (6)
经过Z变换可得
Y(z)=Z-2(Z)+(1-Z-1)2E(Z) (7)
可以看出由一阶调制器的级联而得到的二阶调制器的输出包括输入信号的2个采样周期延迟和量化误差的2阶差分。
由此可以推理得出L阶调制器的传输函数为:
Y(z)=Z-Lx(Z)+(1-Z-1)LE(Z) (8)
令Hk(Z)=Z-L,Fn(Z)=(1-Z-1)L,则信号传输函数为Hk(Z),是L个延时(全通函数),噪声传输函数为Fn(Z),是L阶整形,即高通函数,将量化噪声推向更高的频域。

图4为信噪比随过采样率和阶数的变化。可以看出采样频率每增加2倍,在L=1时,信噪比提高9 dB,L=2时,信噪比提高15 dB,时,信噪比提高21 dB。过采样率以及阶数越高,∑-△调制器的量化信噪比越好。但是过采样率和调制器的阶数不会一直提高,因为现代工艺还未达到这个水平,硬件实现难,而且调制器的阶数过高会造成系统的不稳定,不利于结果的输出。
3 数字抽取滤波原理
∑-△调制器的输出,信号频谱分布在基带内,而量化噪声则分布在基带之外,所以可以利用数字信号低通滤波器来获得想要的输出。而在一般情况下,为了方便以后对输出信号进行处理,则需要将输出信号的频率将至奈奎斯特频率。数字低通滤波器通常分为两类,有限冲击响应滤波器(FIR)和无限冲击响应滤波器(IIR),在降频变换中,通常采用可以获得精确线性相位的FIR数字滤波器。

滤波以后,进行对数据的重采样,它是通过每输出M个数据抽取1/M个数据完成的,这种方法也叫做输出速率降为的采样抽取,即减采样,最终输出频率降至奈奎斯特频率。通常,减采样后的离散序列的频谱将会出现混迭,为了避免混迭,可在信号减采样前用低通滤波器对信号进行滤波,如图5所示,称该低通滤波器为抽取滤波器。一般的,如果低频信号z(n)的频谱是带限的,即在区间[-π,π]范围内有
则M倍减采样后信号的频谱不会发生混叠。式称为序列减采样不混叠的奈奎斯特条件,即奈奎斯特频率为π/M(数字频率)。
若信号x(n)需保留的最高频率分量为ωm/M(ωmπ),即减采样后的信号在频谱范围[0,ωm]内无混叠,在频率范围[ωm,π]允许存在混叠。则抽取滤波器H(z)的幅度响应可为
M倍减采样滤波系统输出信号的时域表达式可写为
由上式可知在计算M倍减采样滤波系统的输出时,只需计算抽取滤波器每M个输出中的一个样本,所以可以减少系统的计算量。通过抽取滤波器以后,我们就可以得到想要的结果了。
4 结束语
高精度是∑-△A/D转换器最突出的优点,其转换精度一般都在16位以上,在相同精度的模数转换器中∑-△A/D转换器价格最低,作为测量系统的核心元件,它会提升整个系统的性价比,而且越来越多的应用于数字信号处理系统中。但是这种转换器也是存在着很多制约其发展的因素,最突出的就是,∑-△A/D转换器以提高采样时间换取精度,应用于对时间要求比较严格的数字信号处理系统比较困难,因此∑-△A/D转换器还有更远的路要走。
&sum -△A/D转换器 -△调制器 过采样 噪声整形 数字抽取滤波 相关文章:
- 基于Zigbee技术家用无线网络的构架(12-14)
- 无线通信领域中的模拟技术发展趋势(蜂窝基站)(09-22)
- 新一代移动通信系统及无线传输关键技术(06-19)
- 蜂窝移动通信基站电磁辐射对人体影响的探讨(04-10)
- 基站升级换代中平衡性能与成本(10-06)
- 在3G与Wi-Fi之间切换 H3C 运营商WLAN解决方案(01-15)
