扩展了信任与隐私的ABAC模型研究

摘要：基于属性的访问控制模型(ABAC)特别适用于大规模分布式网络。然而，由于其访问控制决策依赖于属性的暴露，又没有有效的敏感属性保护机制，使得访问主体的敏感属性存在非法暴露的风险。本文提出了一种扩展了信任与隐私的ABAC模型，它包含了信任与隐私这两个特殊属性，并使访问控制决策敏感于跨组织的协作上下文，以解决ABAC模型本身不含敏感属性保护机制的问题。设计了一种促使管理者在危机管理系统中做出更优决策的图形化原型工具，并验证本文方法的有效性。

编者按：ABAC模型(基于属性的访问控制模型)是业界专为物联网这类分布式环境定制的，用于解决动态分布式环境下的访问控制问题，此模型基础上进行扩展以提供对被访问者的隐私保护机制，防止访问过程中隐私的非法暴露。文中解决了物联网的一个应用实例(协作危机管理)中可靠的访问控制问题，将此方法推广到物联网层面上也是有效的。

引言

近年来，随着大规模分布式网络的广泛使用，网络上出现了大量安全性要求很高的关键服务，如协作危机管理，而这些服务都必须有足够的安全手段来防止非授权的访问。访问控制AC是企业信息安全关注的重心^[1]。而诸如基于角色的访问控制^[2]等传统模型不适用于这类分布式环境中，其原因在于潜在用户众多并且大多数是事先不可知的，此外，其策略表达力、灵活性、可扩展性都不能满足协作危机管理的需要。正因如此，文献^[3]提出了基于属性的访问控制模型ABAC( Attribute-Based Access Control)。ABAC与XACML(eXtensible Access Control Makeup Language)标准密切相关，虽然这种基于属性的方法有更好的灵活性、更细的访问控制粒度和良好的跨域访问控制机制，但其访问决策过程依赖于主体、客体和环境属性的暴露，而ABAC模型本身不具备有效的隐私保护机制，这可能导致在访问控制策略决策阶段访问主体敏感信息的非法暴露。为了解决上述问题，本文在基本的ABAC模型中扩展信任与隐私两个要素，以支持协作危机管理中安全的访问控制。

1 扩展了信任与隐私的ABAC模型介绍

本文所用基本模型的策略决策是基于各访问实体属性的ABAC模型。由于属性作为访问控制粒度的细致性与通用性，几乎所有现有的AC模型都可以在此模型基础上约减得到。

对比于现存的ABAC机制，本文提出的扩展模型包含协作上下文以及对主体集与客体集的信任及敏感属性保护。本文通过在协作环境下加入信任与隐私这两个关键要素，来实现上述的观点。其目的是将这样一个通用模型作为协作危机管理AC授权框架。本文首次将信任、隐私与上下文三个概念结合到ABAC模型中并同时服务于AC的主客体。

图1表述了本文提出的扩展模型的元素关系，该模型包含的基本元素有主体(用户的集合)、客体(资源的集合)、上下文、属性(主体属性AttributeS与客体属性AttributeO)、操作、许可、许可分配函数、信任(主体信任TrustS与客体信任TrustO)及隐私(主体隐私PrivacyS与客体隐私PrivacyO)。

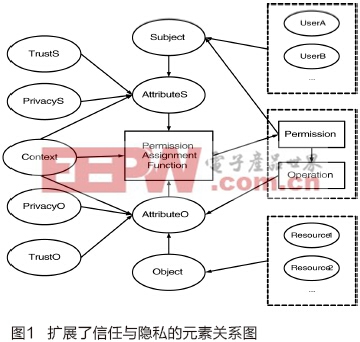
图2是关于用户请求的AC的一个实例。通过该实例说明，当主体试图访问客体属性并做出某种操作时，本文模型在通用工作流中是怎样运作的。在对该操作进行授权或拒绝之前，该用户请求通过该模型被截获，通过评价主客体之间的访问目的的兼容性来保证客体隐私，在特定上下文中通过使用主体与客体的属性来决定ABAC规则的评估结果。

2 扩展了信任与隐私的ABAC授权模型定义

本文的ABAC模型包含属性、主体与主体属性、客体与客体属性、上下文、许可、许可分配函数、操作这几个基本概念，以及信任、隐私这几个扩展概念。

信任：表示某一访问实体对另一访问实体预期行为的主观判断，本文用TrustS与TrustO分别表示主体信任与客体信任。信任度为信任的量化，取值范围为[0,1]。

隐私：表示被访问实体不愿被不可信实体获取的信息，本文用PrivateS与PrivateO分别表示主体隐私与客体隐私。防止访问实体敏感信息被非法暴露的行为叫做隐私保护。

许可分配函数：表示将访问控制策略与规则应用于访问请求的函数，是许可与请求之间的一一映射。一个全局许可分配函数可表示为pa_i()，其中i表示函数标识符，括号内是评估所需各种参数，包括主客体属性集、上下文集合与操作集，评估结果有三种，即前文所述之授权许可集。每条pa_i()评估访问控制策略的一条规则i，并分配访问的某个特定许可，完整形式如公式1所示：

pa_i(s.ATTR, o.ATTR, CTXT , OP) ∈ PER{‘allow’, ’deny’, ’NA’}    　　(公式1)

本文使用函数FACD()来决定最终的访