基于主动控制的自适应同步策略在混沌信号解调中的

摘要：在保密通信领域，对隐藏在混沌信号中的信息解调是一个重要课题。为了有效地解调信息，提出一种基于主动控制的自适应同步策略。利用Lyapunov稳定性理论和Chua电路模型的数值仿真证实了该策略的可行性。仿真结果表朗在接收器上利用这种策略所设计的主动控制器和自适应解调器能够提取隐藏于混沌信号中的传输信息，并且通过提高主动控制器的增益，可以减少由于外部噪声和信息的不连续性造成的误差。
关键词：保密通信；信息解调；主动控制；自适应同步策略；数值仿真

混沌信号以其所固有的难以预测性和对初始值的极端敏感性为混沌在保密通信中的应用提供了前提。美国海军实验室研究人员Pecora和Carroll于1990年首次提出了驱动一响应混沌同步方法以及混沌同步控制理论，这为混沌应用于保密通信提供了理论基础。近十多年来，利用混沌进行保密通信的研究已成为混沌应用研究的一个重要领域。目前已经提出了多种混沌保密通信方案，例如，混沌遮掩法：以混沌信号作为载体来隐藏或遮掩待传送的信息信号；混沌参数调制方法：用信息信号调制混沌系统的参数来实现调制目标；混沌开关键控方法：根据混沌系统在不同参数下具有不同吸引子的特征，把二元信息分别映射到不同的混沌吸引子上以实现保密通信等。

1 保密通信系统
保密通信系统的结构框图如图1所示，其中发射机的驱动系统是一个混沌系统，可以描述为：

式中，状态向量X∈Rn表示传输的信号，μ∈Rm为参数向量，F为一个非线性向量函数，s表示要通过混沌系统加密传输的有用信息。

为了能让该信息安全地到达指定的接收器，必须把它经过混沌驱动系统加密。同时，接收器需要一个专门能检测出混沌信号的响应系统和一个能解密有用信息的解调器。
驱动系统的状态向量可表示为：

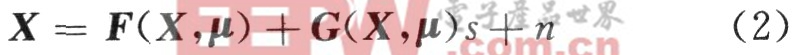
式中，G是一个已知的非线性向量函数，n是外部噪声。
接收器响应系统的状态向量与式(2)相同，对于接收器来说，隐藏于混沌信号中的有用信息是不可知的，所以需要一种专门的解调器去解密。

2 解调信息的自适应同步策略
为了从混沌信号中提取有用信息，需要设计一个控制器u和一套实时更新的规则，来使响应系统和驱动系统中的混沌信号保持同步。控制器响应系统的状态向量可表示为：

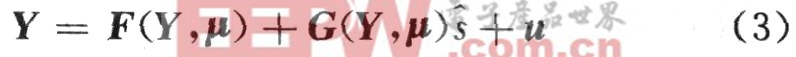
式中，Y是响应系统的输出信号，s是从混沌信号中经过解密得到的有用信息。
式(3)和式(2)之差是响应系统和驱动系统之间的误差，它们之间的关系可表示为：

根据以上分析，提出一种基于主动控制的自适应同步策略，据此来设计控制器和解调器。
控制器的设计如下：

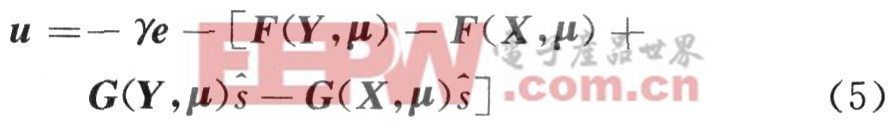
式中，主动控制器的增益γ为正实数。
解调器的设计如下：

接下来根据Lyapunov稳定性理论来研究系统的稳定性。选择如下的Lyapunov函数来分析系统的误差：

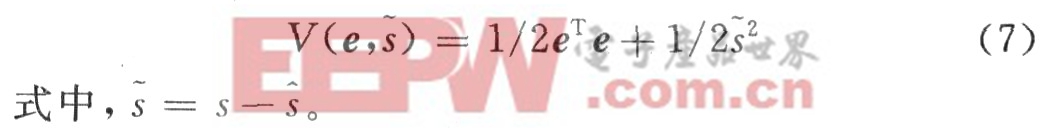
显然，这里的V(e，s)是一个非负函数。根据上述设计的控制器和解调器，可以得出关于V(e，s)的一个推论：

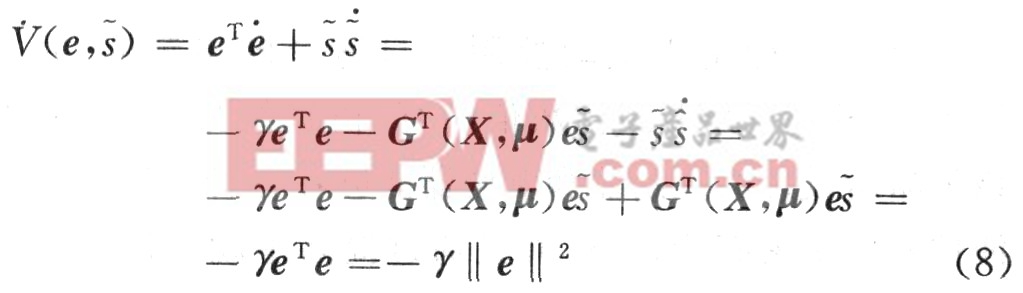
由式(8)可得，当且仅当||e||2=O时，V(e，s)=O，否则会出现V(e，s)0的情况。由此可以推出：当t→∞时，s(t)→s(t)或e→O。这说明解密得到的信息与原始信息非常接近，而且随着时间的推移，系统的误差接近于零，即该误差是大范围渐进稳定的。因此，从理论上讲接收器采用这种设计的控制器和解调器能够从混沌信号中解密有用信息。

3 接收系统的建模与数值仿真
3．1 接收系统的建模
根据Chua电路的传输模型：

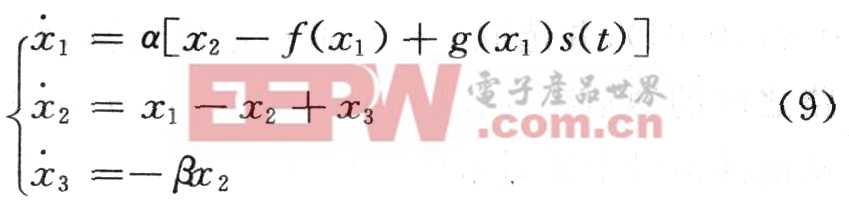
式中，f(x1)=2／7xl一3／14(|x1+1|―|x1―1|)是一个分段线性函数，g(x1)=|x1+1|―|x1一1|。
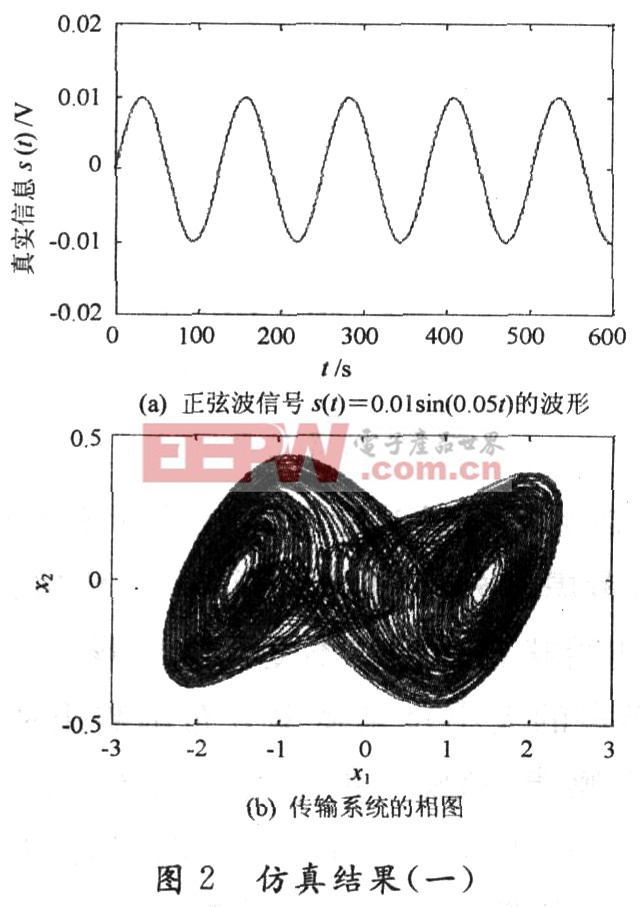
当α=9．0，β=14．286时，上述模型呈现出一种双螺旋特征。令信息为正弦波信号s(t)=O．01sin(Q，05t)，如图2(a)所示。假设Chua电路传输模型的初始条件为(x1(O)，x2(O)，x3(O))=(1，0．01，0．01)。传输系统的相图(x2比x1)如图2(b)所示。由图2(b)可以看出该传输系统是混沌系统。因此，包含信息s(t)的混沌信号和不包含信息s(t)的混沌信号是很难进行区分的。

根据上述的主动控制自适应同步策略，接收器模型建立如下：

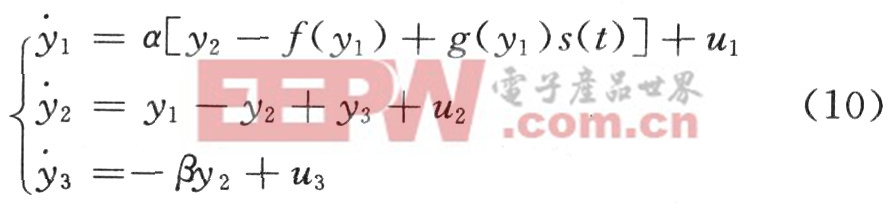
根据式(5)，控制器的参数模型向量u=[u1，u2，u3]T的设计如下：

3．2 无噪声混沌系统的连续信号数值仿真与结果分析
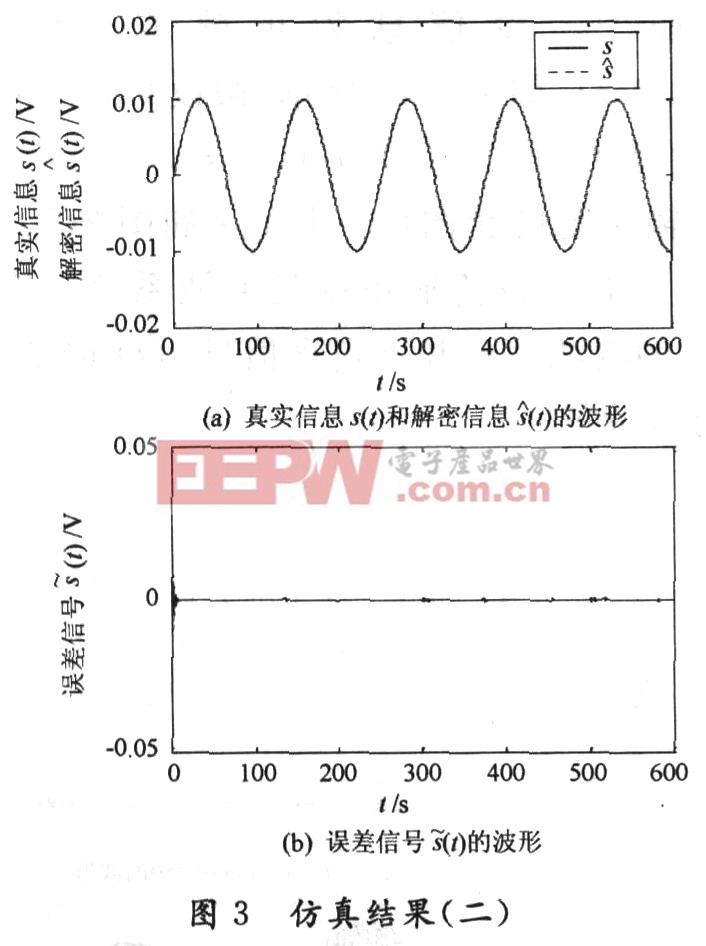
首先，假设在没有噪声的情况下，传输的信息为图2(a)所示的正弦波信号s(t)=0．01sin(O．05t)，响应系统的初始状态为(y1(O)，y2(O)，y3(0))=(一1，0．01，O．01)，并选取γ=1，通过数值仿真，两个Chua电路之间的通信特性如图3(a)所示。从图3(a)可以看到从混沌信号中通过解密所得到的信息s(t)与真实信息s(t)几乎是完全重合的。从图3(b)可以看到随着时间的推移，误差信号s(t)=s(t)一s(t)迅速降低到几乎接近于零的值。

3．3 带噪混沌系统的连续信号数值仿真