无重叠生成文法的一义可解析性及图林等价性

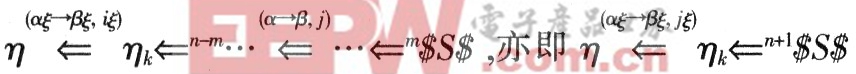
显然，n+1和ηk对于iξ是唯一的。

无回朔一义可解析性表明．对于推导句型中的任意位置的逆用项可以在任何需要的时候应用它而不会改变解析的成功。任何解析步中出现的逆用项也可以被同时并行替换。

5 OFG的解析算法
根据定理4．1，可以直接得到如下异常简单的解析算法，其对于OFG全集可无回朔一义解析。
算法5．1
(1)cw=$x$，x是一个被解析的字。
(2)if cw=$s$则成功解析并终止。
(3)随机地在cw中找一逆用项(α→β,i)，且将其应用于
cw，这里α→β,∈P。如果无逆用项则解析失败并终止。
(4)跳到(2)。
定理5．1 x在L(G)中当且仅当算法5．1终止并成功解析。
证明：由无回朔一义可解析性定理可证明。
算法中采用了随机选择的策略，也可以使用最左优先或任意的解析策略。

6 结论
根据上面的讨论，0FG具有下列性质：
OFG具有通用性(与图灵机等价性)(定理3．1)，
OFG具有一义可解析性(定理4．1)，
OFG存在十分简单的解析算法(算法5．1)。
需要进一步讨论的问题是能否找到有用的OFG文法子集，在该子集上实现更有效的解析。另一个问题是希望能找到CFG与0FG子集的转换关系，因为CFG的简明方便性，与CFG对应的OFG文法将有较广泛的应用。