基于Cyclone Ⅲ的CCK调制、解调全新电路研究与实现

由图1可知，输入的比特流首先被划分成8个比特一组。每组中的高6位(d7，d6，…，d2)用来从基本码字库(共有64个CCK码字)中惟一选取一个CCK码字。之后，再用前2个比特(d0，d1)来确定φ1，并将对其产生的码字进行DQPSK调制，最后产生I，Q两路调制信号，完成CCK扩频调制。
CCK实现的原理图如图2所示。这个模块由两大部分组成，数据流1：8串并转换模块和CCK调制模块。

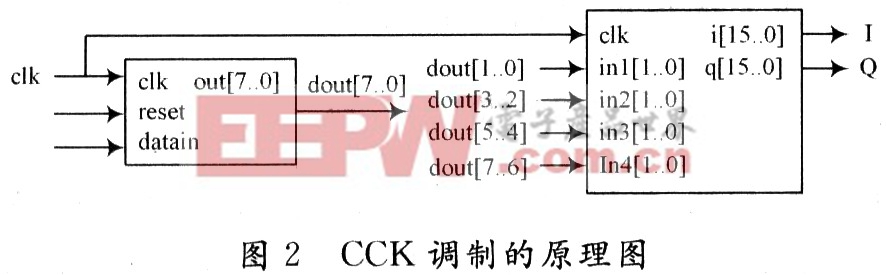
CCK调制的具体实现如上文所述，其仿真结果如图3所示。

2．3 CCK的解调
2．3．1 最大似然解码
在对CCK的进行解调时，一般可采用最大似然解码器对码字进行解码，这里的最大似然(ML)解码器是利用CCK码字的良好的互相关特性，将接收到的受到噪声干扰的码字与64个可能的码字进行相关运算，然后比较得到64个相关结果，并找出其中幅度值最大的那一个，由此对码字作出判决。
设接收到的CCK码字为C'={C0，C1，C2，C3，C4，C5，C6，C7}；Ci(i=0，1，…，7)表示接收到的数据，将其与所有码字进行相关运算，则R=C'C*，C*是C的共轭，C是发送端的码字，则：

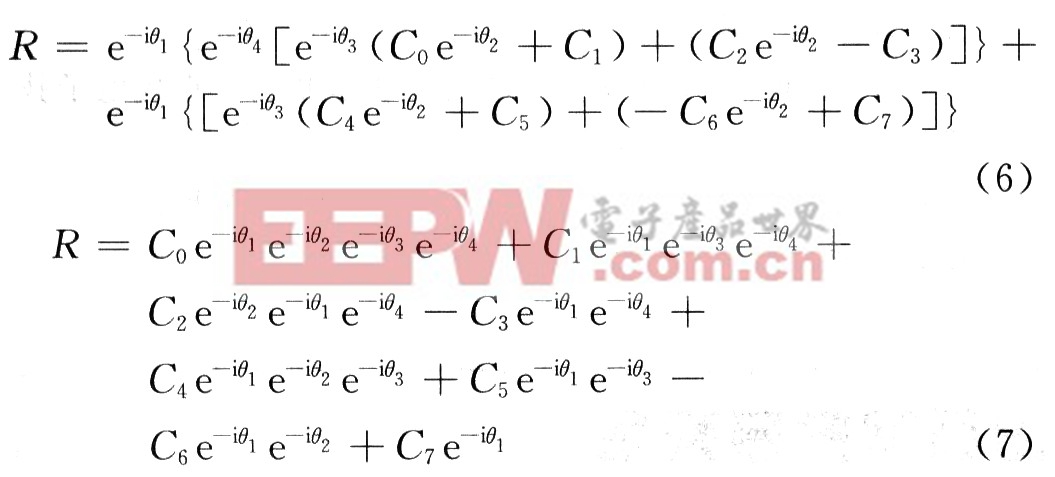
式中：θi(i=1，2，3，4)表示角度；θ1～θ4遍历{0，π／2，π，3π／2}。由式(7)可知，只有当θ2=φ2，θ3=φ3，θ4=φ4时，相关值会获得最大值，为8，并由此解调出d7～d0的值。
2．3．2 新的解码方法――选择部分解码
通过上述内容可以看出，如果对调制后的CCK码字C'={C0，C1，C2，C3，C4，C5，C6，C7)中的每一位进行相关运算，并且在对每一位进行运算时，又对其中的θ1～θ4都进行遍历{0，π／2，π，3π／2)的话，解调过程将是一个很复杂而又繁琐的过程，同时它所带来的计算量也将是巨大的。所以，这里提出一种全新的CCK解调方案。
这种全新的解调方案不像传统的解调方案那样对每个CCK调制后的码字进行相关运算，再根据相关值最大来判断出相应的CCK码，而是只对部分的调制后的CCK码字进行相关运算，并根据相关最大值解调出全部的CCK码。
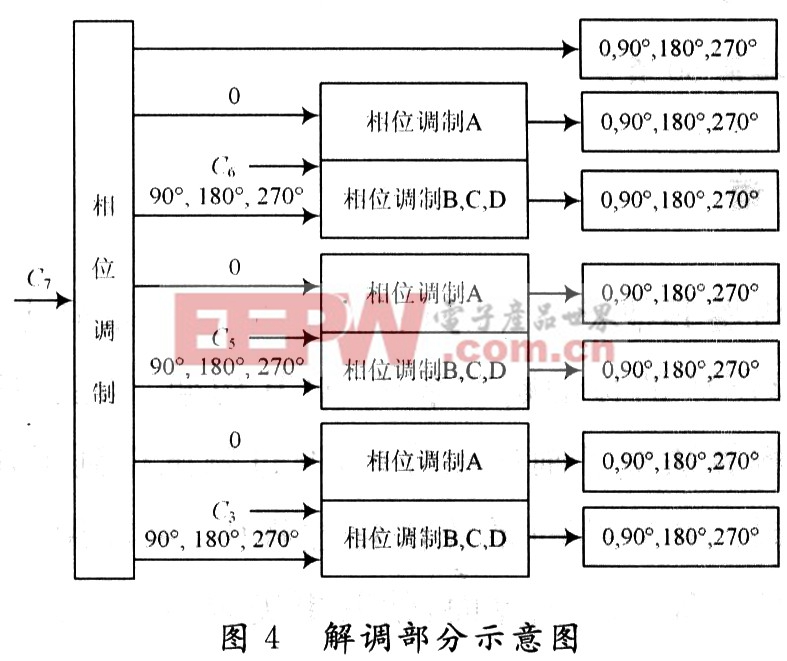
通过观察式(7)可以看到，调制后的码字C'={C0，C1，C2，C3，C4，C5，C6，C7}，其中的C7与e-iθ1进行相关运算，根据最大峰值在相关结果中的位置，可确定θ1的值，也即解调出了φ1(φ1=θ1)，然后再按照表1来确定d0，d1。码字C中G是与一e“q。。吃’进行相关运算的，如果其中臼。的值已经确定，那么可以在岛为定值的情况下，根据相关解调的方法，确定岛的值；同理，G是与e’。∞t。如’进行相关运算的，G是与一e-“q也’进行相关运算的，可以通过类似C6的解调方法来确定夙，乱的值，由此也即知道了仰，仲，铆的值(岛一仇，晚一卿，乱一似)，最后根据表2得到d。～d，的值。与其他的ccK解调方案相比，这种解调方案很好地简化了计算过程，也减少了计算的工作量。图4是解调部分的图形表示。

CCK解调实现的原理图如图5所示。这个模块由ccK解调模块和并串模块两大部分组成。

经过CCK解调，得到8位并行数据，再经由并／串转换转换成串行数据输出。

3 结 语
研究了补码序列的定义和性质，并对CCK调制和解调原理进行了分析，提出了更为简便、新颖的CCK调制解调方法，该方法降低了计算的复杂度，同时也大大减少了计算的工作量。本文还将该方法运用VerilogHDL硬件描述语言，通过QuartusⅡ7．2进行了功能仿真和时序仿真，同时还利用Altera公司最新的Cy-clone Ⅲ芯片EP3C25F324C8NES予以实现。CycloneⅢ前所未有地同时实现了低功耗、低成本和高性能。CycloneⅢ的系统最高频率为505．05 MHz，I／O脚最高频率为379．36 MHz，而类似型号的CycloneⅡ，Cyclone工的系统最高频率分别为490．68 MHz和404．53 MHz，I／O脚最高频率分别为91．76 MHz和204．25 MHz，CycloneⅢ的这一特性提高了系统的性能。同时该方案的实现只需用到97个逻辑单元，对CycloneⅢ总逻辑单元，其使用率为0．34％，而类似型号的CycloneⅡ，Cyclone I芯片的逻辑单元，其使用率分别为0．52％和0.48％。由此可见，这种全新方案节省了硬件资源，提高了CCK调制、解调的速率，简化了计算过程，减少了计算量，同时Verilog HDL语言的运用，也增加了描述的灵活性和高效性。