低噪声低失真音频低通滤波器的设计

本文针对音频系统，采用GIC方法，设计出了高性能的低通滤波器．
　　在任何一个量化系统中，防混叠滤波器可以使被采样的信号从无限带宽变为有限带宽，并将不需要的信号从量化系统中消除，从而防止信号频率在采样频率附近发生混叠．在通常情况下，能很好完成这一功能的滤波器大都是很复杂的高阶滤波器．
　　随着转换系统的采样频率增加，过采样技术可以达到降低滤波器抑制频率衰减的技术要求．例如在数字音频系统中，一般可以采用4倍过采样技术，在A／D转换之前可以使用一个6阶防混叠滤波器；对D／A转换器来说，在DAC的后面要采用3阶滤波器，才能达到防混叠的技术要求．然而，要以低失真、低噪声实现这些3阶或6阶滤波器技术要求将是很困难的．

1　广义阻抗变换滤波器的特点
　　用广义阻抗变换的拓扑结构来设计滤波器，给设计者带来了很多方便，可以使设计者很容易地从无源滤波器的设计中实现有源滤波器的功能；广义阻抗变换滤波器具有非常好的低失真、低噪声的特性，且价格也较合理，与人们熟悉的反馈滤波器相比（例如Sallen＆Key滤波器拓扑结构），有更好的噪声和增益特性，非常适合在音频系统
和DSP系统中应用；GIC滤波器有很好的线性相位特性，在音频系统中采用这种滤波器可以大大改善声音质量．
2　无源网络滤波器及其有源变换
　　本设计是基于一个3阶线性相位低通无源T型滤波器，其拓扑结构如图1所示．这是一个截止频率ω＝1 r／s的归一化设计，它既不是Butterworth响应，也不是Bessel响应，而是一个介于二者之间的滤波器．

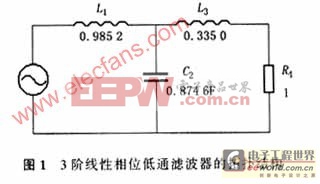
通过计算机模拟和经验分析，找到了线性相位和截止频率衰减等性能得到优化的元件值．将这个无源网络所有的元件乘以1／s因子，图1的无源网络就变为有源网络，所有的电感变成电阻，所有的电阻变成电容，所有的电容变成依赖频率的负阻抗（FDNR）．这些负阻抗的特性阻抗为1／（s2 C）．电路中的负阻抗可以用广义合成阻抗（GIC）电路来实现．
　　这样L1变成R1，C2变成1／（s2 C），L3变成R3，R4变成C4．如图2所示．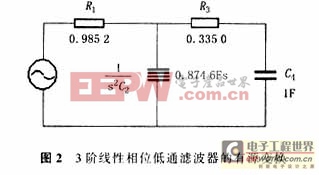


3　有源网络的实现及参数确定
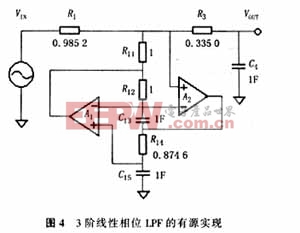
　　图2中1／s2 C是一个依赖频率的负阻抗，可以采用布鲁吞（Bruton）提出的广义合成阻抗（GIC）电路来实现．其电路如图3所示．

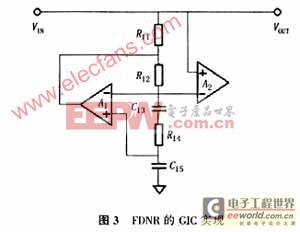
　　其中，FDNR的值为：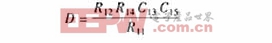

　　假设R11＝R12＝1，C13＝C15＝1，那么D的值仅由R14来决定．对于图2的FDNR电路来说，R14＝0．874 6Ω．
　　整个3阶滤波器如图4所示．这种无源网络的有源实现是针对截止频率ω＝1 r／s的电路设计的．为了使滤波器具有我们所期望的截止频率，必须按照理想的截止频率和合理的元件值对各元件值进行修正．对于音频设计来说，截止频率为20kHz．但是，线性相位滤波器衰减较慢，在截止频率之前的通带内要引起1～2dB的衰减；而通常的音频系统频率响应达到20kHz，并且通带内的衰减要控制在0．1dB以内．因此，在音频系统中，防混频滤波器的截止频率一般设为40kHz才能达到
要求．若截止频率取40kHz，电路中所有电容都要除以频率标定因子2πfc，使1F电容值变为3．98μF．由于大电容和小电阻给实际应用设计带来困难，因此，电路中的电阻要进行阻值变换．当电阻值变化时，电容值也要作相应的调整，这样才能保证滤波器的截止频率保持不变．
　　其方法为：首先，选定易于购买的小电容值，然后，将电路中的所有电阻乘以阻抗调整因子β，β值由下式确定：

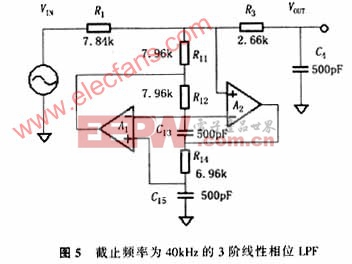
　　按照上述方法，若理想电容取500pF，则阻抗因子为7 960，电路中的各元件值变为如图5所示．这样，既保证了截止频率不变，又解决了大电容、小电阻等问题．

　　要想得到截止频率为40kHz 6阶线性相位低通滤波器也很容易，只要将图5所示的3阶低通滤波器经缓冲器隔离之后级联就可以实现，如图6所示．其频率特性如图7所示．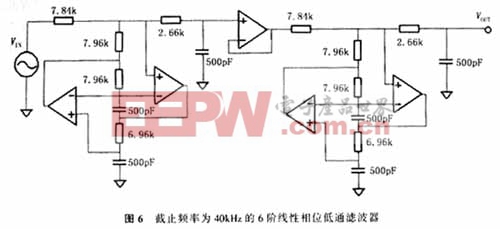

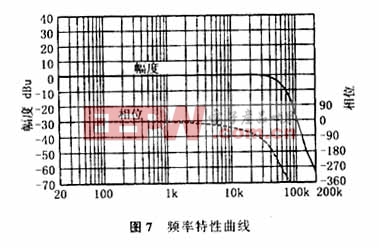
　　从频率特性曲线可以看出滤波器通带增益平坦，相位线性度较好，从而使语音信号通过滤波器后的失真很小，保证了语音信号的高质量．
4　结束语
基于广义合成阻抗方法的滤波器与传统的反馈滤波器相比，不仅增益、线性相位和低噪声等性能优良，而且使设计变得更加方便，减少了许多计算量．本文就音频系统应用中的低通滤波器的设计，给出了3阶和6阶低通滤波器的设计实例．实例方法可以推广应用到其他任意截止频率高阶低滤波器的设计中，这对于设计高性能低通滤波器是十分有益的．