Buck变换器的数字模糊PID控制

摘要：由Buck电路的状态空间平均法，可得到其电压控制下的动态小信号模型，并应用PID实现其精确控制。为提高控制精度和抗干扰能力，用模糊控制器对PID参数进行实时整定，给出了仿真与实验结果及结论。关键词：Buck变换器；状态空间平均法；模糊控制；PID控制

1引言

在DC/DC变换器中，电压反馈控制因具有设计分析较简单、低阻抗功率输出、负载调整率较好等优点,而被广泛应用于DC/DC变换器中。其缺点是任何输入电压或输出负载的变化必须首先转化为输出电压的变化，然后再经反馈环采样控制调节，这意味着动态反应速度慢。输入电压变化带来的问题，一般可采用电压前馈技术解决。而要获得系统的快速性，主要有以下方案可供选择： 1）引入电流负反馈；

2）在主电路中增加阻尼极点或补偿极点；

3）提高开关频率以减小低通滤波器电感或电容

值；

4）采用PID调节。

其中唯有4）采用PID调节是较为可行的方法[1]。但单纯的PID调节对于处理DC/DC变换器的非线性等问题不够理想。模糊控制正好可以弥补这方面的不足。

近年来，随着芯片技术的不断发展，特别是DSP芯片价格的下降和速度的提高，DC/DC变换器控制技术正向着数字化、智能化控制方向发展。这是开关稳压电源高精度控制发展的必然趋势，也是21世纪开关稳压电源研究的一个重要课题。

考虑到以上各种因素，本文以Buck电路为例，介绍电压反馈控制模式下,DC/DC变换器系统数字模糊PID控制的原理、方法与实现。

2Buck电路动态小信号分析

考虑实际电感和电容存在电阻值，设分别为RL、RC(如图1所示)。根据状态空间平均法，可得到Buck电路的状态平均方程为：=AX＋BUin（1）

Uout=CX（2）式中：X=；

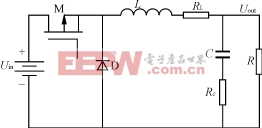
图1 Buck变换器电路拓扑图

图2Buck变换器开环控制方框图

(b)PID控制系统的频率特性

图3系统开环及使用PID控制的频率特性BODE图

A=；B=；C=；
Uin为输入直流电压；

Uout为输出电压。引入小信号变量：x=X＋，uin=Uin＋，及d=D＋代入式（1）得：=A＋B＋E（3）式中：E=；

D为占空比。

式（3）即为Buck电路动态小信号状态平均方程,将式（3）转换到s域并解之，可得到电压反馈控制下动态小信号模型的传递函数：=（4）

3模糊PID控制实现由式（4）可知，电压反馈控制为二阶系统，而二阶系统是一个有条件的稳定系统，只有对控制电路进行精心设计和计算，满足一定条件，才能使闭环系统稳定工作。考虑到输入电压变化量和占空比变化量(s)均对输出有影响，变换器系统的开环控制框图如图2所示。

图中N(s)为变换器输出对d(s)而言的系统开环传递函数，G1(s)可由（4）得出：G1(s)=

在电压负反馈控制中，如果引入输入电压前馈校正控制环，就能消除输入电压波动对系统的干扰，进而很好地改善系统的控制性能。为进一步提高控制性能与精度，控制电路采用具有微分和积分控制作用的数字PID控制。PID控制器中微分控制能预测事物的变化趋势，可以补偿由低通滤波器引起的时间滞后；积分控制能消除系统静态误差。从而采用PID控制，能增加系统的快速性和有效抑制超调，使系统动态性能和控制精度得以改善。由系统的BODE图（图3）可以看

(a)开环系统的频率特性

()开关电源

(a)系统输入电压阶跃变化(b)受扰动电压负反馈控制波动图

(c)受扰动PID控制波动图(d)受扰动模糊PID控制波动图

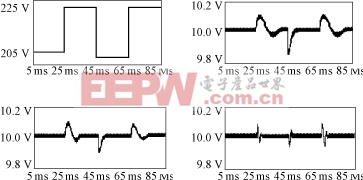
图6仿真结果

Buck变换器的数字模糊PID控制

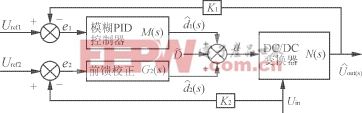
图4Buck变换器模糊PID闭环控制框图

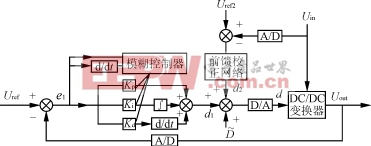
图5Buck变换器模糊PID控制框图

出，系统开环的频率特性较差，采用PID控制后，不仅改善了系统的相角裕度，同时也降低了系统在低频时的增益。应用模糊控制对PID参数Kp、Ki、Kd实时地进行整定，则能改善PID的控制性能、自调整能力，从而可提高整个系统的控制精度和抗干扰能力。

3.1控制电路设计系统的闭环控制框图如图4所示。取输出电压的误差和微分量，送入模糊控制器和PID控制器，由模糊控制器根据输入控制量偏差实时给出PID的参数，再由PID控制器给出控制信号，从而实现对变换器的精确控制。取输入电压的误差送入系统前馈校正电路中，输出补偿量加入到模糊PID控制输出量，和一起组成变换器的占空比控制量d。图中：Uref2、Uref1分别为输入和输出参考电压；采用上一周期的输出占空比值，而不用静态值D，这样可确保系统的平滑性和稳定性；M(s)为模糊PID控制器的传递函数；G2(s)为前馈补偿函数。

3.2PID参数的整定

对于线性系统，PID参数的整定方法有多种，如：

1）ZieglerNichols频率响应法[2]；

2）Cohencoon响应曲线法[3]；

3）基于积分平方准则ISE整定法[4]；

4）极点配置法；

5)根轨迹法；

6)工程整定法等等。

实际上，DC/DC变换器为一非线性系统，而