一类可变参数数字均衡器的设计

3．1 一阶低频均衡处理后的结果图
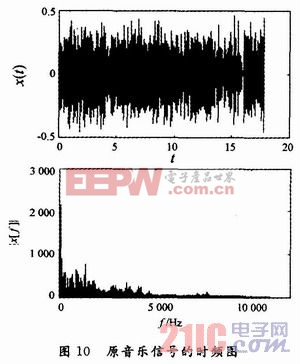
设定一阶低频均衡器的参数K=2．5，α=0．4和K=2．5，α=0．8对处理后的音乐信号时域用Y(t)表示，频域用Y(f)表示。源音乐信号做均衡处理，处理后的结果如图11所示。

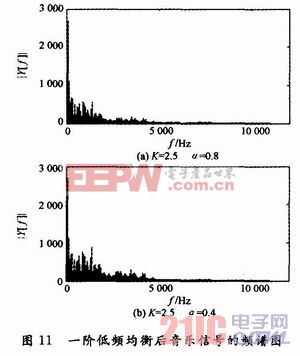
由图11可知，均衡后低频部分的幅度都有所增大，由K控制，α=0．8时，均衡的频率范围大约是0～2 000 Hz，而α=0．4时均衡的频率范围大约为0～4 000 Hz，由此可知，参数α的变化控制均衡的带宽范围，α越大，均衡器截止频率越小。试听均衡后的信号，音量变大，低频部分增加，音乐变得厚重、雄浑，二者音色均发生变化。
3．2 一阶高频均衡处理后的结果图
设定一阶高频均衡器的参数K=2．5，α=0．8和K=2．5，α=0．2对源音乐信号做均衡处理，处理后的结果如图12所示。

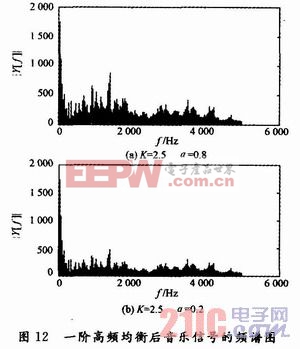
当设定均衡器参数为K=2．5，a=0．8，频谱特性幅度增大的频率范围是音乐信号的高频部分，大约在1 200～5 000 Hz，而对信号的低频部分没有影响；K=2．5，α=0．2，频谱特性高频幅度增大的频率范围为3 500～5 000 Hz。试听均衡后的音乐信号，音量变大，整体音调变高，α越大，均衡器截止频率越小，音色发生变化的效果不同。
3．3 二阶均衡处理后的结果图
设定二阶均衡器的参数分别为K=3．5，α=0．4，β=-0．8；K=3．5，α=0．4，β=0．4和K=3．5，α=0．8，β=0．4，对原音乐信号作均衡处理，处理后的结构图如图13和图14所示。

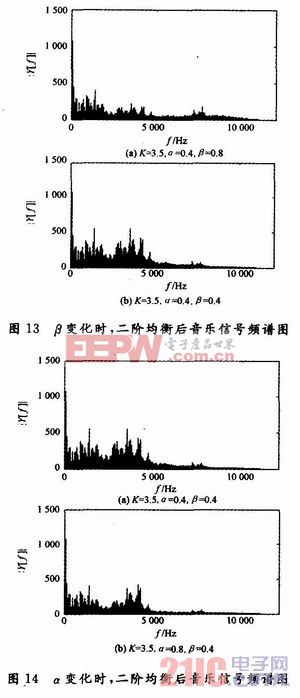
在图13(a)中，音乐信号的频谱在5 000～11 000 Hz的频率范围内幅度增大，在大约8 000 Hz的地方出现了一个谐振峰，在图13(b)中，音乐信号的频谱在2 000～8 000 Hz的频率范围内幅度增大，而在频率大约为4 000 Hz的地方出现了一个谐振峰。由此可见，α相同，带宽相同，但是β不同，出现谐振峰的频率位置不同，由此证明参数β控制谐振峰出现的位置。
在图14(b)中，均衡后音乐信号幅度增大的频率范围大约在4 000～6 000 Hz内，与图14(a)相比，均衡的带宽变小，但谐振峰出现的位置相同，大约都在4 000 Hz的地方。结果表明，调节参数α时，带宽变化，当α增大时，带宽变小；当α减小时，带宽反而变大，β不变，谐振峰位置不变。

4 结语
对音乐信号处理的参数可变数字均衡器的设计进行了研究，给出了数字均衡器的数学模型，分析了各数字均衡器的频响特性随参数变化的情况。一阶的高、低频均衡器有两个可变参数K和α，分别控制数字均衡器频响的幅度大小和截止频率(即带宽)，二阶数字均衡器有三个可变参数K，α和β，分别控制均衡器频响的幅度大小、带宽和谐振峰的位置。通过实例进行了论证分析，得出的结果表明，灵活地设定均衡器的各参数可以设计出满足音乐信号处理频响需求的数字均衡器，达到改善音乐信号音质的目的，这种方法简单、灵活、可行。