组合逻辑电路的分析与设计-逻辑代数
量取值相异(一个为0,另一个为1)时,输出函数值为1。
在MOS门电路中 ,我们已接触过异或门,上面的推导更明确地告诉我们,异或门和同或门互为非函数。所以在异或门电路的输出端再加一级反相器,也能得到同或门,如下图所示。
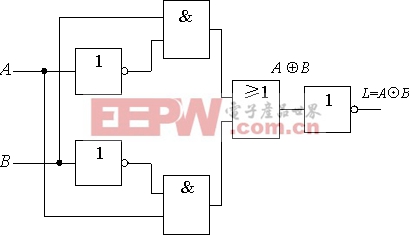
至此,我们已经学到了不止一种同或函数,但是同或函数的真值表却是唯一的,事实上还可以列举许多。由此可以得出结论:一个特定的逻辑问题,对应的真值表是唯一的,但实现它的电路多种多样。这给设计电路带来了方便,当我们手头缺少某种逻辑门的器件时,可以通过函数表达式的变换,避免使用这种器件而改用其他器件。这种情形在实际工作中常会遇到。
2.逻辑函数的化简
根据逻辑表达式,可以画出相应的逻辑图。但是直接根据某种逻辑要求而归纳出来的逻辑表达式及其对应的逻辑图,往往并不是最简的形式,这就需要对逻辑表达式进行化简。
一个逻辑函数可以有多种不同的逻辑表达式,如与—或表达式、或—与表达式、与非—与非表达式、或非—或非表达式以及与—或—非表达式等。

以上五个式子是同一函数不同形式的最简表达式。以下将着重讨论与或表达式的化简,因为与或表达式易于从真值表直接写出,且只需运用一次摩根定律就可以从最简与或表达式变换为与非一与非表达式,从而可以用与非门电路来实现。
最简与或表达式有以下两个特点:
①与项(即乘积项)的个数最少。
②每个乘积项中变量的个数最少。
代数法化简逻辑函数是运用逻辑代数的基本定律和恒等式进行化简,常用下列方法:
① 并项法

② 吸收法

③ 消去法
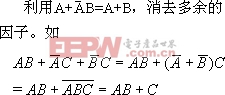
④ 配项法

使用配项的方法要有一定的经验,否则越配越繁。通常对逻辑表达式进行化简,要综合使用上述技巧。以下再举几例。
例1 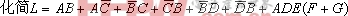
解:

例2 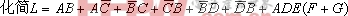


模拟电路 模拟芯片 德州仪器 放大器 ADI 模拟电子 相关文章:
- 12位串行A/D转换器MAX187的应用(10-06)
- AGC中频放大器设计(下)(10-07)
- 低功耗、3V工作电压、精度0.05% 的A/D变换器(10-09)
- PIC16C5X单片机睡眠状态的键唤醒方法(11-16)
- 用简化方法对高可用性系统中的电源进行数字化管理(10-02)
- 利用GM6801实现智能快速充电器设计(11-20)
