逻辑函数的卡诺图化简法

号——对应，可以得到下面这种形式的卡诺图。

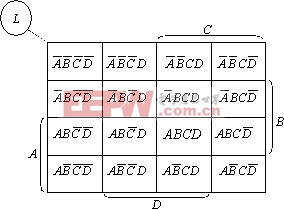
2.卡诺图的特点

　　上面所得各种变量的卡诺图，其共同特点是可以直接观察相邻项
。也就是说，各小方格对应于各变量不同的组合，而且上下左右在几何上相邻的方格内只有一个因子有差别，这个重要特点成为卡诺图化简逻辑函数的主要依据。在卡诺图水平方向的同一行里，最左和最右端的方格也是符合上述相邻规律的，例如，m₄和m₆的差别仅在C和。同样，垂直方向同一列里最上端和最下端两个方格也是相邻的，这是因为都只有一个因子有差别。这个特点说明卡诺图呈现循环邻接的特性。

3.已知逻辑函数画卡诺图

　　根据逻辑函数的最小项表达式和卡诺图的一般形式，就可以得到相应的卡诺图。
　例如，要画出逻辑函数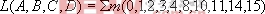的卡诺图时，可根据４变量卡诺图，对上列逻辑函数最小项表达式中的各项，在卡诺图相应方格内填入１，其余填入０，即可得到如下图所示的Ｌ的卡诺图。

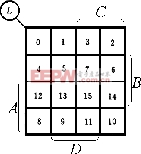
例：画出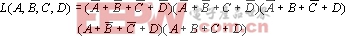
的卡诺图
解：
　　（1）利用摩根定律，可以将上式化简为：

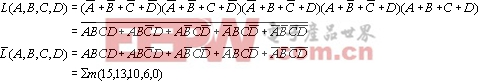
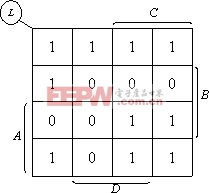
　　（2）因上式中最小项之和为Ｌ，故对Ｌ中的各最小项，在卡诺图相应方格内应填入０，其余填入１，即得下图所示的卡诺图。

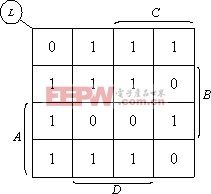
四、用卡诺图化简逻辑函数

1.化简的依据

　　我们知道，卡诺图具有循环邻接的特性，若图中两个相邻的方格均为1，则这两个相邻最小项的和将消去一个变量。
　　比如４变量卡诺图中的方格５和方格７，它们的逻辑加是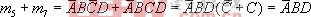，项消去了变量Ｃ，即消去了相邻方格中不相同的那个因子。若卡诺图中４个相邻的方格为１，则这４个相邻的最小项的和将消去两个变量，如上述４变量卡诺图中的方格２、３、７、６，它们的逻辑加是

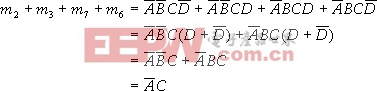
　　消去了变量Ｂ和Ｄ，即消去相邻４个方格中不相同的那两个因子
，这样反复应用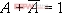的关系，就可使逻辑表达式得到简化。这就是利用卡诺图法化简逻辑函数的某本原理。

2.化简的步骤

用卡诺图化简逻辑函数的步骤如下：
　　（1）将逻辑函数写成最小项表达式。
　　（2）按最小项表达式填卡诺图 ，凡式中包含了的最小项，其对应方格填1，其余方格填0。
　　（3）合并最小项，即将相邻的1方格圈成一组（包围圈），每一组含2ⁿ个方格，对应每个包围圈写成一个新的乘积项。
　　（4）将所有包围圈对应的乘积项相加。
　　有时也可以由真值表直接填卡诺图，以上的（1）、（2）两步就合为一步。

画包围圈时应遵循以下原则：
　　（1）包围圈内的方格数必定是2ⁿ个，n等于0、1、2、3、…。
　　（2）相邻方格包括上下底相邻，左右边相邻和四角相邻。
　　（3）同一方格可以被不同的包围圈重复包围 ，但新增包围圈中一定要有新的方格，否则该包围圈为多余。
　　（4）包围圈内的方格数要尽可能多，包围圈的数目要尽可能少。

　　化简后，一个包围圈对应一个与项（乘积项），包围圈越大，所得乘积项中的变量越少。实际上，如果做到了使每个包围圈尽可能大
，结果包围圈个数也就会少，使得消失的乘积项个数也越多，就可以获得最简的逻辑函数表达式。下面通过举列来熟悉用卡诺图化简逻辑函数的方法。

　　例: 一个逻辑电路的输入是４个逻辑变量Ａ、Ｂ、Ｃ、Ｄ ，它的真值表如下，用卡诺图法求化简的与一或表达式及与非一与非表达式。

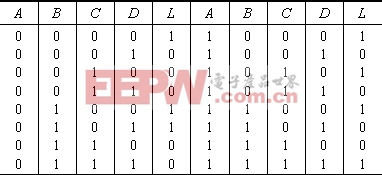
解：
　　（1）由真值表画出卡诺图，如下图所示。

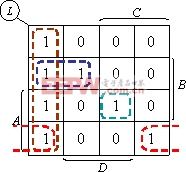
　　（2）画包围圈合并最小项，得简化的与一或表达式。

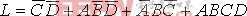
　　（3） 求与非一与非表达式。

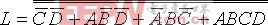
　　二次求非然后利用摩根定律得

　　利用卡诺图表示逻辑函数式时，如果卡诺图中各小方格被１占去了大部分，虽然可用包围１的方法进行化简，但由于要重复利用１项
，往往显得零乱而易出错。这时采用包围０的方法化简更为简单。即求出非函数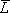再对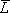求非，其结果相同，下面举例说明。

例：化简下列逻辑函数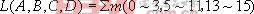

解：
　　（1）由Ｌ画出卡诺图，如图所示。

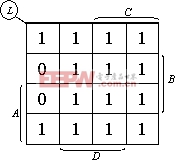
　　（2）用包围１的方法化简，如下图所示，得

　　所以有：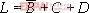

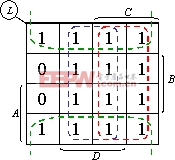
　　（3）用包围０的方法化简，如图所示，

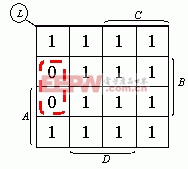
　　根据图得到：，两边去反后可得：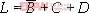
　　两种方法得到的结果是相同的。
　　实际中经常会遇到这样的问题，在真值表内对应于变量的某些取值下，函数的值可以是任意的，或者这些变量的取值根本不会出现，这些变量取值所对应的最小项称为无关项或任意项。
　　无关项的意义在于，它的值可以取０或取１，具体取什么值，可以根据使函数尽量得到简化而定。