Σ-ΔADC转换器工作原理及应用分析

越来越多的应用，例如过程控制、称重等，都需要高分辨率、高集成度和低价格的ADC。 新型Σ-Δ转换技术恰好可以满足这些要求。然而，很多设计者对于这种转换技术并不十分了解，因而更愿意选用传统的逐次比较ADC。Σ-Δ转换器中的模拟部分非常简单(类似于一个1bit ADC)，而数字部分要复杂得多，按照功能可划分为数字滤波和抽取单元。由于更接近于一个数字器件，Σ-ΔADC的制造成本非常低廉。

　　一、Σ-ΔADC工作原理

　　要理解Σ-ΔADC的工作原理，首先应对以下概念有所了解：过采样、噪声成形、数字滤波和抽取。

　　1. 过采样

　　首先，考虑一个传统ADC的频域传输特性。输入一个正弦信号，然后以频率fs采样--按照 Nyquist定理，采样频率至少两倍于输入信号。从FFT分析结果可以看到，一个单音和一系列频率分布于DC到fs /2间的随机噪声。这就是所谓的量化噪声，主要是由于有限的ADC分辨率而造成的。单音信号的幅度和所有频率噪声的RMS幅度之和的比值就是信号噪声比(SNR)。对于一个Nbit ADC，SNR可由公式：SNR=6.02N+1.76dB得到。为了改善SNR和更为精确地再现输入信号，对于传统ADC来讲，必须增加位数。

　　如果将采样频率提高一个过采样系数k，即采样频率为kfs，再来讨论同样的问题。FFT分析显示噪声基线降低了，SNR值未变，但噪声能量分散到一个更宽的频率范围。Σ-Δ转换器正是利用了这一原理，具体方法是紧接着1bit ADC之后进行数字滤波。大部分噪声被数字滤波器滤掉，这样，RMS噪声就降低了，从而一个低分辨率ADC，Σ-Δ转换器也可获得宽动态范围。

　　那么，简单的过采样和滤波是如何改善SNR的呢?一个1bit ADC的SNR为7.78dB(6.02+1.76)，每4倍过采样将使SNR增加6dB，SNR每增加6dB等效于分辨率增加1bit。这样，采用1bit ADC进行64倍过采样就能获得4bit分辨率;而要获得16bit分辨率就必须进行415倍过采样，这是不切实际的。Σ-Δ转换器采用噪声成形技术消除了这种局限，每4倍过采样系数可增加高于6dB的信噪比。

　　2. 噪声成形

　　通过图1所示的一阶Σ-Δ调制器的工作原理，可以理解噪声成形的工作机制。

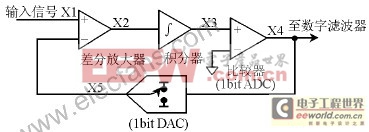
　　图1 Σ-Δ调制器

　　Σ-Δ调制器包含1个差分放大器、1个积分器、1个比较器以及1个由1bit DAC(1个简单的开关，可以将差分放大器的反相输入接到正或负参考电压)构成的反馈环。反馈DAC的作用是使积分器的平均输出电压接近于比较器的参考电平。调制器输出中"1"的密度将正比于输入信号，如果输入电压上升，比较器必须产生更多数量的"1"，反之亦然。积分器用来对误差电压求和，对于输入信号表现为一个低通滤波器，而对于量化噪声则表现为高通滤波。这样，大部分量化噪声就被推向更高的频段。和前面的简单过采样相比，总的噪声功率没有改变，但噪声的分布发生了变化。

　　现在，如果对噪声成形后的Σ-Δ调制器输出进行数字滤波，将有可能移走比简单过采样中更多的噪声。这种调制器(一阶)在每两倍的过采样率下可提供9dB的SNR改善。

　　在Σ-Δ调制器中采用更多的积分与求和环节，可以提供更高阶数的量化噪声成形。例如，一个二阶Σ-Δ调制器在每两倍的过采样率下可改善SNR 15dB。图2显示了Σ-Δ调制器的阶数、过采样率和能够获得的SNR三者之间的关系。

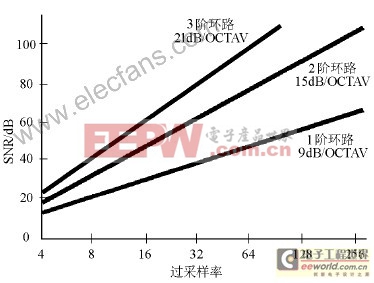
　　图2 SNR与过采样率的关系

　　3. 数字滤波和抽取

　　Σ-Δ调制器以采样速率输出1bit数据流，频率可高达MHz量级。数字滤波和抽取的目的是从该数据流中提取出有用的信息，并将数据速率降低到可用的水平。

　　Σ-ΔADC中的数字滤波器对1bit数据流求平均，移去带外量化噪声并改善ADC的分辨率。数字滤波器决定了信号带宽、建立时间和阻带抑制。

Σ-Δ转换器中广泛采用的滤波器拓扑是SINC3，一种具有低通特性的滤波器。这种滤波器的一个主要优点是具有陷波特性，可以将陷波点设在和电力线相同的频率，抑制其干扰。陷波点直接相关于输出数据速率(转换时间的倒数)。SINC3滤波器的建立时间三倍于转换时间。例如，陷波点设在60Hz时(60Hz数据速率)，建立时间为3/60Hz=50ms。有些应用要求更快的建立时间，而对分辨率的要求较低。对于这些应用，新型ADC诸如MAX1400系列允许用户选择滤波器类型SINC1或SINC3。SINC1滤波器的建立时间只有一个数据周期，对于前面的举例则为1/60Hz=16.7ms。由于带宽被输出数字滤波器降低，输出数据 速率可低于原始采样速率，但仍满足Nyquist定律。这可通过保留某些采样而丢弃其余采样来实现，这个过程就是所谓的按M因子"抽取"。M因子为抽取比例，可以是任何整数值。在选择抽取因子时应该使输出数据速率高于两倍的信号带宽。这样，如果以fs的频率对输入信号采样，滤波