频率响应法-- 频域性能指标和时域性能指标的关
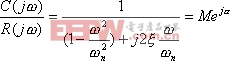 |
|
式中
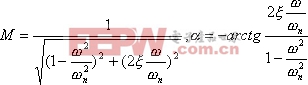 |
当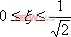 时,系统有谐振产生,由本章第三节讨论可知,其谐振峰值分别为
时,系统有谐振产生,由本章第三节讨论可知,其谐振峰值分别为
 |
|
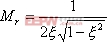 |
|
由式(5-70)得
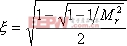 |
|
1、谐振峰值![]() 和最大超调量
和最大超调量![]() 的关系
的关系
为了便于对谐振峰值![]() 和最大超调量
和最大超调量![]() 作比较,把
作比较,把![]() 和
和![]() 与
与![]() 的关系曲线都画在图5-65中。由图可见,
的关系曲线都画在图5-65中。由图可见,![]() 和
和![]() 均随着
均随着![]() 的减小而增大。显然,对于同一个系统,若在时域内的
的减小而增大。显然,对于同一个系统,若在时域内的![]() 大,则在频域中的
大,则在频域中的![]() 必然也是大的;反之亦然。为了使系统具有良好的相对稳定性,在设计系统时,通常取
必然也是大的;反之亦然。为了使系统具有良好的相对稳定性,在设计系统时,通常取![]() 值在
值在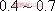 之间,对应的
之间,对应的![]() 将坐落在
将坐落在![]() 之间。
之间。
把式(5-70)代入式(5-63),则得
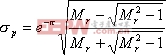 |
|
如果已知![]() ,则由上式可求得对应的
,则由上式可求得对应的![]() 。
。
 |
| 图5-65 谐振峰值 和最大超调量 的关系 |
 |
| 图5-66 |
2、谐振峰值![]() 和调整时间
和调整时间![]() 、峰值时间
、峰值时间![]() 关系
关系
根据在第三章中导出二阶系统的上升时间和调整时间的关系式,并考虑到式(5-69),则得
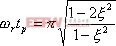 |
|
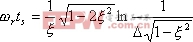 |
|
由式(5-70)有:
 |
|
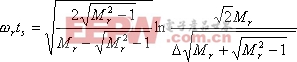 |
|
将式(5-75)的函数关系用曲线表示,如图5-66。可见,峰值时间![]() 与谐振峰值
与谐振峰值 ![]() 成正比,而峰值时间
成正比,而峰值时间![]() 与谐振频率
与谐振频率![]() 成反比。调整时间
成反比。调整时间![]() 与
与![]() 和
和![]() 的关系和峰值时间
的关系和峰值时间![]() 与它们的关系相同。同时上述两式表明,如果已知
与它们的关系相同。同时上述两式表明,如果已知![]() 和
和 ![]() ,就能从上述关系式中求出
,就能从上述关系式中求出![]() 和
和 ![]() 。
。
3、频带宽度与峰值时间、调整时间的关系
根据频带宽度的定义,当![]() 时,二阶系统的幅频为
时,二阶系统的幅频为
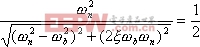 |
求解上式,得
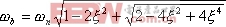 |
|
同理,注意到式(5-73)、(5-74),并对照式(5-69),则得
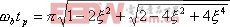 |
|
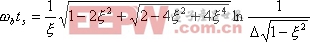 |
|
由式(5-78)和(5-79)可知,对于给定的![]() ,
, ![]() 和
和![]() 均与
均与![]() 成反比。这就是说,
成反比。这就是说,![]() 越大,则系统响应的速度就越快。
越大,则系统响应的速度就越快。
把式(5-70)代入式(5-78)、(5-79),可求得
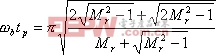 |
|
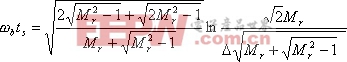 |
|
上述两式把时域性能指标![]() 、
、![]() 与频域性能指标
与频域性能指标![]() 和
和![]() 联系起来,如果已知
联系起来,如果已知![]() 和
和![]() ,就能从上述关系式中求出
,就能从上述关系式中求出![]() 和
和![]() 。
。
对于高阶系统,系统的频率响应与时域响应间的对应关系可通过经验公式联系,也通过傅氏积分,即,
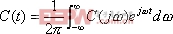 |
|
由于这种积分变换较复杂,因而不可能像二阶系统那样简单地描述频域响应与时域响应间的对应关系,其积分一般借助于计算机辅助算法,且目前这些算法均比较成熟。如果高阶系统中有一对共轭主导极点,则上述二阶系统的时域响应与频域响应间的对应关系就可近似地应用于高阶系统中去。
模拟电路 模拟芯片 德州仪器 放大器 ADI 模拟电子 相关文章:
- 12位串行A/D转换器MAX187的应用(10-06)
- AGC中频放大器设计(下)(10-07)
- 低功耗、3V工作电压、精度0.05% 的A/D变换器(10-09)
- PIC16C5X单片机睡眠状态的键唤醒方法(11-16)
- 用简化方法对高可用性系统中的电源进行数字化管理(10-02)
- 利用GM6801实现智能快速充电器设计(11-20)

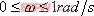 ,系统Ⅱ的带宽为
,系统Ⅱ的带宽为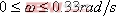 ,即系统I的带宽是系统Ⅱ带宽的三倍。图5-64b表示了两系统的阶跃响应曲线。显然,系统I较系统Ⅱ具有较快的阶跃响应,并且前者跟踪阶跃输入的性能也明显优于后者。
,即系统I的带宽是系统Ⅱ带宽的三倍。图5-64b表示了两系统的阶跃响应曲线。显然,系统I较系统Ⅱ具有较快的阶跃响应,并且前者跟踪阶跃输入的性能也明显优于后者。