基于RFID高速公路车辆测速定位方案

fd 值则需要进行实时估计。因此，对fd 估计的准确程度是实现精确定位的关键。

3 多普勒频移fd 的估计

　　近年来，已有多种fd 估计算法被提出，如在时域中利用电平通过率进行直接测量［3］、或采用时频分析方法［4］、或利用一些特殊性质如OFDM 导频信号来估计最大多普勒频移［5］。

　　这些方法要么测量精度过低，要么运算量过大，均不适合在RFID 系统中应用。本文结合RFID 系统特点，采用功率谱估计的方法，在频域实现对fd 的估计。

　　由于在车辆移动过程中，车载阅读器与标签之间的相对位置是不断变化的，因此时域采样点数应尽量少，以保证fd值的相对稳定。现代谱估计方法在短数据记录的情况下，其性能远远优于经典谱估计方法。其中，Burg 算法不需要估计自相关函数，具有较高的谱估计质量且计算不太复杂，是较为通用的方法，亦适合在RFID 系统中使用。

　　对将接收信号进行下变频并等间隔时域采样，得到信号序列x（1）， x（2），……， x（n） 。采用Burg 算法进行谱估计，并利用反射系数公式中的递推关系减小运算量，同时使用信息论准则法判定AR 模型阶数P.

　　算法基本步骤为：

　　（1）设定初始条件。令第0 阶前向、后向预测误差序列为时域采样序列。

　　（2）设定阶数m=1，则得到反射系数k1 、模型参数a1（1）及最小预测误差功率ρ1 。

　　（3）由反射系数k 1 得到第一阶前、后向预测误差序列 e1 f （n），e1 b （n）。

　　（4）令m = m+1，采用递推分母DENm求出该阶反射系数km 及最小预测误差功率。

　　（5）采用信息论准则法判定阶数P.令AICm = N ln（ρm） +2m ，其中，N为数据x（n） 的长度。当阶次m由1增加时，AICm应在某一m 处达到最小值。因此， 若测得在m 阶有1 AICm《AIC m-1 ，则说明尚未达到AR 模型的正确阶次。否则，转到（7）。

　　（6）计算m 阶前、后向预测误差序列 emf（n） 、emb（n） 及所有模型参数am （i）， i = 1，2，……，m，返回（4）。

　　（7）当AICm ≥AIC m-1 时，说明m-1 即为AR 模型的正确阶次，至此，已求出所有阶次时的AR 参数，可对AR 模型的功率谱进行估计。

　　（8）得到功率谱后，找到其幅值最大值所对应的频率值，即为fd 值，算法结束。

　　算法流程如图3 所示。

　　图3 Burg 算法流程

　　4 算法求解

　　4.1 牛顿迭代法

　　将式（1）~式（4）联立并化简，可得到如下方程：

　　将式（5）写成矩阵形式：

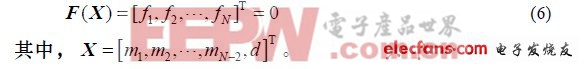
　　采用牛顿迭代法，设已得到第k 次近似解Xk，则可得：

　　式（7）即为式（6）的牛顿迭代公式，采用Gauss-Jordan 方法求解Jacobi 矩阵DF（Xk）的逆，则可求得X，确定车辆的实时位置。再将结果代入式（5），即可得到车辆速度v.

　　4.2 初值设定

　　由于牛顿迭代法是局部收敛的，因此选定的初值要接近方程的解，否则有可能得不到收敛的结果。因此，合理地选取初值，不仅能确保求解过程不发散，而且还能减少迭代次数，进而减少算法运算量。

　　根据式（3）可知，相邻射频卡p、p+1 分别在车载阅读器行驶方向的法线两侧。因此，可设：

　　依次可设：

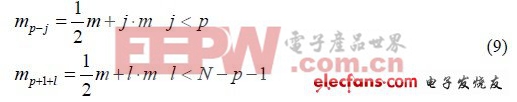
　　此外，由图2 还可知2dr + dl 》 d 》 dl 。

5 仿真实验

　　仿真模型见图2，设路肩宽度dl=2 m，车道宽度dr=5 m，每2 个射频卡之间距离m=5 m，RFID 系统工作频率f=915 MHz，阅读器和射频卡的最大通信距离R=14 m，采样频率fs=1 600 Hz，采样点数N=128.考虑到高速公路环境较为空旷，忽略多径干扰的影响，但由于阅读器的接收信号十分微弱，因此干扰噪声对其影响较大，设置信噪比SNB=-5 dB。

　　针对不同多普勒频移随机实验500 次，其结果如表1 所示（限于篇幅，选取部分数据罗列）。可以看出，本文所采用的谱估计方法具有较高的估计精度，误差在0.8 Hz 以下，且随着fd 值不断增大，误差值呈减小的趋势。

　　分别设定v 为30 km/h、60 km/h、90 km/h、120 km/h、150 km/h，针对不同位置对车辆速度进行反复测量，其平均误差如表2 所示。当车辆接近静止时，由于不存在多普勒频移或多普勒频移十分微小，由系统设定v=0.随着车辆移动速度的提高，由于多普勒频移在夹角一定的情况下同速度呈正比，因此速度误差会随着fd 测量误差的减小略呈下降趋势。

　　图4 给出了400 次定位结果误差分布。可以看到，节点位置误差基本上在0.3 m 之内，平均误差为0.1 m 左右。

　　表1 fd 估计值及误差 Hz.

　　表2 速度平均估计值及误差

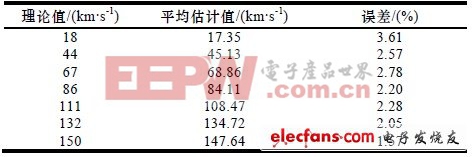
　　图4 定位结果误差分布

　　6 结束语

本文针对我国现有高速公路管理系统无法对车辆进行实时管理这一现状，提出一种对高速公路上车辆进行实时测速及定位的方法。该方法具有运算量孝精度高、实施简单的特点，可用于实现高速公路上对车辆的实时跟踪监控。本文仅是将RFID 技术应用于高速公路测速及定位方向的一个简单尝