趋肤效应简介

对于每个电气参数，必须考虑其数值有效时的频率范围。传输线的串联电阻也不例外。与其他参数一样，它也是频率的函数。图4.10画出了RG-58/U和等效串联电阻与频率的函数曲线。图中采用对数坐标轴。图4.10以相同的坐标轴绘出了感抗WL的曲线。

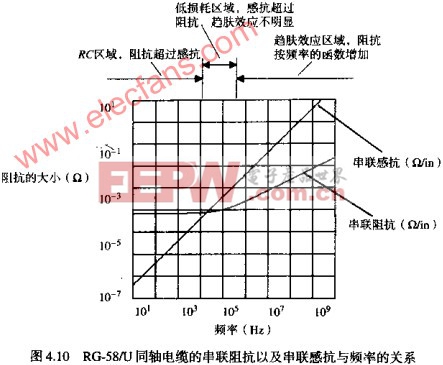
当频率低于W=R/L时，电阻超过感抗，电缆表现为一个RC传输线。当频率高于W=R/L时，电缆是一个低损耗传输线。

当频率高于0.1MHZ时，串联电阻开始增大。这导致更多的衰减，但相位保持线性。这种电阻的增加称为趋肤效应（SKIN EFFECT）。

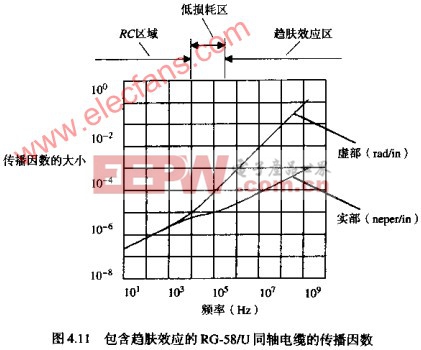
传播因数的实部和虚部（（R+JWL）（JWC））1/2在图4.11中绘出，损耗单位为标培，相位单位为RAD（弧度）。1奈培等于8.69DB的损耗。图中显示了RC区域、固定衰减区域和趋肤效应区域。如图所示，相对于RC区域和趋肤效应区域，低损耗区域非常窄。

是什么导致了趋肤效应，它与导体外表层有什么关系呢？

1、趋肤效应的机理

在低频时，电流在导体内部的分布密度是均匀的。从导线的截面图看，中心和边缘区域电流的流量是相同的。

在高频时，导线表面的电流密度变大，而中心区域几乎没有电流流过。电流分布的变化如图4.12所示，低频时电流均匀地填满整个导线，高频时电流只从接近导线表面的地方流过。

为了形象地证明高频条件下电流的分布，首先假设导线纵向切成多层同心的长管，就像树桩上的年轮。

自然对称的形状可以阻止电流在环间流动，所以必须无误差地切割，所有电流绝对平行于导线的中心轴。

现在导线被切成许多环，我们可以分别考虑每个环的电感。靠近中心的环，像长而薄的管道，比外部的环有更大的电感。我们知道，在高频条件下，电流将从电感更低的通路流过。因此，高频条件下可以预计从外环通路流过的电流比内环更多。实际上正是如此。在高频条件下，绝大多数的电流聚集在靠近导体的外表面。

趋肤效应的作用力甚至比仅仅基于各个环管电感的预测作用更显著，实际上，环管间的互感也迫使电流紧贴着导线的外表面流过。

电流渗透的平均深度，称为趋肤深度。在高频条件下，趋肤深度是相当薄的。随着向内部的接近，在趋肤效应作用下，导体内部电流密度按指数规律下降，平均电流深度是频率W、导体的磁介系数U、电阻系数P的函数：

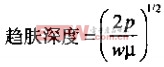
由于大多数电流在导体表面附近的一个薄的管道中流动，可以想象这个导体的视在电阻会大大增加。增加的大小是趋肤深度的函数。导体的视在电阻与电流流经的深度成反比。上式表明，趋肤深度与频率的平方根成反比。综合这些因素，导体的AC电阻与频率的平方根成正比增长。

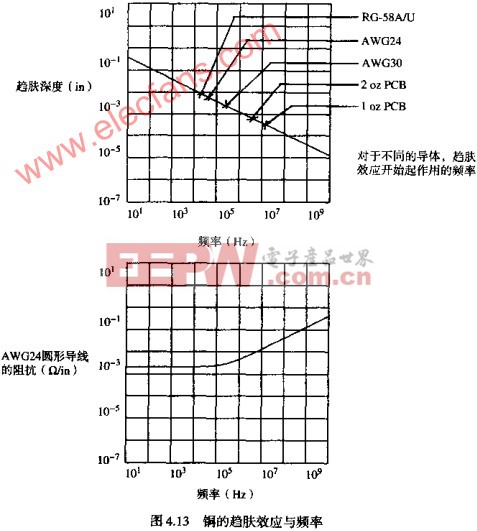
趋肤深度是材料的一个属性，随导体材料的整体导电率的不同而变化。它不是导体形状的函数。图4.13绘出了铜的趋肤深度与频率的函数曲线。图4.13中的第二条曲线给出了AWG24图形铜导线的电阻相对于频率的变化。当频率足够低时，趋肤深度等于或大于导线的半径，我们只考虑导线的总DC阻抗（电流分布在整个导体内）。当趋肤深度小于导线半径时，每个英寸的电阻与频率的平方根成正比增长。下式给出了趋肤深度在有限范围内的电阻。

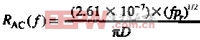
其中，D=线路直径，IN
RAC=AC阻抗，Ω/IN
PR=相对电阻系数（相对于铜）铜=1.00
F=频率，HZ

在实践中，运用上式存在的问题是，低频时得出的电阻值为零。我们知道，直流时导线电阻是一个非零值。下式试图将AC和DC电阻模型合并到一个公式中。对于该复合模型，没有一个封闭型的解：下式仅仅是一个有用的近似。

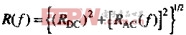
这一方程工更好地模拟了物理现实：低频时电阻保持常数，高频时电阻随频率的平方根成正比增长。电阻开始增长时的频率，等于趋肤深度开始小于导体厚度时的频率。对于圆形导体临界深度等于导体半径。对于扁平的矩形导体，例如印刷电路板走线，临界深度为导体厚度的一半。

对于方形导体，采用上两式时，用方形导体的周长替代πD，以英寸为单位。

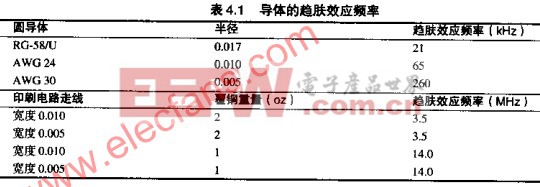
表4.1列出了各种导体中趋肤效应开始起作用的频率。

如果趋肤效应是一种表面化现象，那么增大表面面积应该对趋肤效应有所帮助。LITZ电缆正是这样做的。一段LITZ电缆多股导线构成，每股导线彼此之间都是绝缘的，以特定的绞合方式编织到一起。这一绞合保证了每股导线都受一同样大小的磁力作用，使得每股导线中流过的电流相等。多股导线使总表面积增大，降低了趋肤效应的电阻。LITZ电缆用于巨型超导电电磁线圈以及频率可达1MHZ的电机转子中。超过这个频率，使每股导线中的电流保持均衡就变得几乎不可能了。

2、趋肤效应区的频率响应

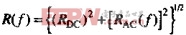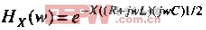用式（）替代式（）中的R，可以预测出工作在趋肤效应区的传输线的衰减和相移。

以DB为单位的传输损耗与电阻成正比，式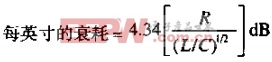（）。电阻与频率的平方根成正比。所以衰减的分贝数必然与频率的平方根成正比。这一结果清楚地显示在RG-174/U衰减曲线中，见图4.14。