LMS自适应滤波器干扰方法

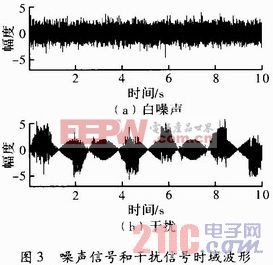
在有用信号S(t)中分别混入高斯白噪声和设计的干扰信号，分别送入自适应滤波器，对滤波器的输出时域波形进行分析，从图4中可以观察LMS算法对混入信号中干扰与噪声的滤除效果，并在图5中比对在有、无干扰作用下自适应滤波器的学习曲线。

随迭代次数增多而下降，经过300～400次迭代后趋于稳定。在干扰信号J(t)作用下，如图5(a)所示，均方误差不随迭代次数增多而逐渐减小，而是呈周期性变化，且其平均值较单一高斯噪声下LMS滤波器的均方误差大。将干扰信号J(t)和噪声n(t)叠加后，滤波器的均方误差同样不递减，具体波形见图5(b)，均方误差随迭代运算次数增多变化平缓。

3 结束语
自适应滤波器由于对外界的信号具有适应能力，可根据外界输入的统计特性实时更新自身结构以实现最小均方误差滤波，具有一定的抗干扰性能。但也存在诸如依赖于统计平稳信号，收敛性能受制于步长大小，响应的滞后性等缺点。文中针对LMS自适应滤波器的步长适应范围的局限性，使用两种统计特性不同的噪声调幅信号交替工作构成干扰，经过仿真验证，可发现所设计的干扰信号可有效降低了自适应滤波器的收敛效率，实现一定的干扰效果。利用自适应滤波器收敛的滞后性缺点能否设计出干扰波形还有待于进一步研究。