光纤光栅传感器的原理及应用

　0 引言

　　近年来。随着光纤通信技术向着超高速、大容量通信系统的方向发展，以及逐步向全光网络的演进.在光通信迅猛发展的带动下，光纤光栅已成为发展最为迅速的光纤无光源器件之一。光纤在紫外光强激光照射下，利用光纤纤芯的光敏感特性.光纤的折射率将随光强的空间分布发生相应的变化。这样，在光纤轴向上就会形成周期性的折射率波动，即为光纤光栅。由于光纤光栅具有高灵敏度、低损耗、易制作、性能稳定可靠、易与系统及其它光纤器件连接等优点，因而在光通信、光纤传感等领域得到了广泛应用。为此。本文从光纤布拉格光栅、长周期光纤光栅等光纤光栅的原理出发，综述了光纤布拉格光栅对温度、应变同时测量技术的应用。

　　1 光纤传感器的工作原理

　　1.1光纤光栅传感器的结构

　　光纤布拉格光栅FBG于1978年发明问世。它利用硅光纤的紫外光敏性写入光纤芯内，从而在光纤上形成周期性的光栅，故称为光纤光栅。图l所示是其光纤光栅传感器的典型结构。

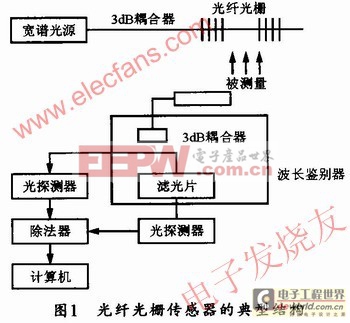
　　在图1所示的光纤光栅传感器结构中，光源为宽谱光源且有足够大的功率，以保证光栅反射信号良好的信噪比。一般选用侧面发光二极管ELED的原因是其耦合进单模光纤的光功率至少为50～100 μW。而当被测温度或压力加在光纤光栅上时。由光纤光栅反射回的光信号可通过3 dB光纤定向耦合器送到波长鉴别器或波长分析器，然后通过光探测器进行光电转换，最后由计算机进行分析、储存，并按用户规定的格式在计算机上显示出被测量的大小。

　　光纤光栅除了具备光纤传感器的全部优点外.还具有在一根光纤内集成多个传感器复用的特点，并可实现多点测量功能。

　　1.2 光纤布拉格光栅原理

　　光纤布拉格光栅通常满足布拉格条件

　　式中，λB为Bragg波长，n为有效折射率，A为光栅周期。

　　当作用于光纤光栅的被测物理量(如温度、应力等)发生变化时，会引起n和A的相应改变，从而导致λB的漂移;反过来，通过检测λB的漂移。也可得知被测物理量的信息。Bragg光纤光栅传感器的研究主要集中在温度和应力的准分布式测量上。温度和应力的变化所引起的λB漂移可表示为：

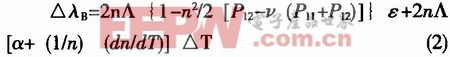
　　式中，ε为应力，P[i，j]为光压系数，v为横向变型系数(泊松比)，α为热胀系数，△T为温度变化量。一般情况下， (2)式中的n2[P12-v(P11+P12)]/2因子的典型值为0.22，可以推导出常温和常应力条件下的FBG温度和应力相应条件值为：

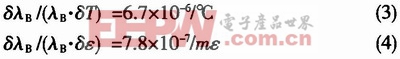
　　利用磁场诱导的左右旋极化波的折射率变化的不同，可实现对磁场的直接测量。如通过在光栅上涂敷特定的功能材料(如压电材料)，可实现对电场等物理量的间接测量。

　　1.3 长周期光纤光栅

　　长周期光纤光栅(LPG)是一种新型的光纤光栅，光栅周期一般大于100μm，是继FBG之后光纤光栅型传感器的另一分支。长周期光栅的透射峰波长主要与光栅的栅格周期以及纤芯和包层的折射率有关，其相位匹配条件可表示为：

　　式中。Λ为光栅周期，*****分别为纤芯和包层的折射率。*****为第P阶包层模的透射波长。当光纤包层模与外界环境相互作用时，被测因素的变化将对光纤的传输特性进行调制，从而使LPG的透射谱特性发生变化。这样，探测出LPG透射谱线的变化，即可推知被测变量的变化，这就是LPG传感的基本原理。

　　1.4 分布式光纤光栅传感系统

　　目前，除光纤光栅型传感器的原理性研究之外，分布式光纤传感系统也是一个重要的研究重点。分布式FBG传感系统是在一根光纤中串接多个FBG传感器，每个光栅的工作波长相互分开，在经过3 dB耦合器取出反射后，再用波长探测解调系统同时对多个光栅的波长偏移进行测量，从而检测出相应被测量的大小和空间分布。

　　分布式光纤传感系统是一种传感器网络，它可以从整体上对被测对象的有关物理量的变化时间、位置进行监控。通过对分布式光纤传感器、执行结构、信号处理系统、传输系统和控制系统的结合，可形成一个智能结构。目前，分布式光纤传感系统通常有拉曼型、布里渊型和FBG型三种类型。

　　2 温度和应变交叉敏感分离技术

　　实现应变和温度同时测量的方案很多，但是从原理上分析，基本都是基于双波长矩阵法、双参量矩阵法、温度参考光栅法、温度(应力)补偿法和光强测温法等几种技术。

　　2.1 双波长矩阵法

　　双波长矩阵法是出现较早而且目前应用较为广泛的一种方案。其基本思想是通过一定方式在一个传感头中获得两个不同的布拉格波长，并通过检测这两个布拉格波长的位移来实现温度不敏感测量或应变及温度的同时测量。如果λ1、λ2同时对两被测量比较敏感。且波长漂移随温度和应变的变化为线性，温度和应变变化独立或只有微弱扰动，则由下式可得：

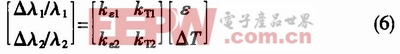
式中，kTi为布拉格波长的应变灵敏系数，它与光纤泊松比