陶瓷谐振原理及在红外遥控电路中的设计应用

陶瓷谐振电路的基本原理和结构

陶瓷谐振的特性

陶瓷谐振器类似于石英晶体，是一个压电器件，可以把电能转换为机械能，也可以把机械能转换为电能。当外加的交流电场的频率和谐振器的谐振频率发生共振时，电能和机械能的转换会发生在谐振器的谐振频率上。陶瓷谐振器具有对激励信号频率十分敏感的突出特点。

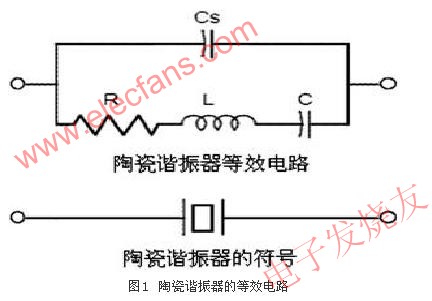
在电路分析中，陶瓷谐振器的等效电路如图1所示，其中Cs为静电电容，R为振荡损耗等效电阻，C为弹性等效电容，L为机械振动等效电感。



振荡电路

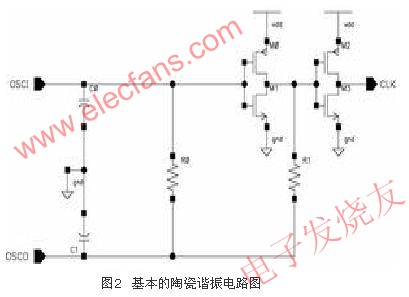
本设计采用的陶瓷谐振电路的电路原理图如图2所示。其中M0和M1一起构成反相放大器，提供振荡电路所需要的180度相移;OSCI和OS

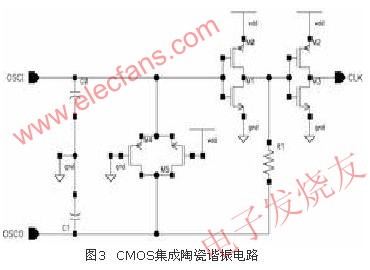
CO两端接陶瓷谐振器，和C0、C1一起构成选频网络，同时再次提供180度相移;R0是反馈电阻，为放大器的输入提供偏置;R1为相位补偿电阻，其大小由M0和M1的尺寸决定，在频率比较低的应用中，R1甚至可以为0。选用不同特征频率的陶瓷谐振器后，这个电路就可以产生相应的振荡频率。M2和M3构成输出缓冲电路，可以增大振荡器的振荡幅度和负载能力，同时把振荡整理成方波形式输出。由于反馈电阻R0一般较大，为106欧姆级，所以在CMOS集成电路设计中，常用传输门代替此电阻，减少芯片面积，降低功耗，如图3所示。





红外遥控电路中陶瓷谐振电路的设计

为了节省资源，提高产品的竞争力，在振荡电路的设计中，所用结构要尽量简单，要把电容集成到芯片内部。因为电容在芯片中占的面积相对较大，所以电容要尽量小，但又必须让电路能振荡。带控制端的陶瓷谐振电路如图4所示。



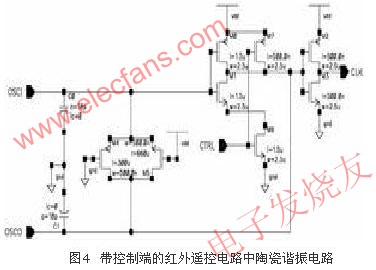
一般，在红外遥控发射电路中，振荡部分有一个标识按键的使能信号CTRL。一旦有按键，CTRL信号为1，则M7关断，M1和M6等效为一个N管，与M0共同构成振荡反相器;当无按键时，CTRL为0，M7导通，把输出缓冲的输入电平钳位到高电平，数字时钟输出为低，系统停振，这样做的目的是为了在无按键时降低功耗，同时可以使遥控芯片内的时序不至于混乱。

OSCI和OSCO外接455kHz陶瓷谐振器(红外遥控电路的振荡频率一般都为455kHz)。电路中采用大长宽比的传输门做反馈电阻，这样可以减少面积，提高性能，减少用n+层做电阻时的对偏效应，而且降低功耗。由于半导体中电子迁移率大约为空穴迁移率的2倍，为了做到N管和P管对称，P管的宽长比一般大约为N管的2倍，所以在此传输门电阻中，N管的尺寸为0.5/300，P管为0.5/660。同理，反相放大器中M0、M1、M6尺寸均为2.5/1.5，M1和M6构成大致为2.5/3的N管(暂称为M1-6)。输出缓冲M2和M3采用制造厂家的标准库参数尺寸，都为2.5/0.5。由于振荡频率不是很高，所以电阻R1可以去掉。C0和C1的大小决定着整个电路的大小，它们取值相等，最小值取18pF。

电路中作为反相放大器的M0和M1-6的尺寸比较重要，流片中试验了3种尺寸，测试结果如表1所示。表中Vppl和Vpph分别指振荡波形的最小电压值和最大电压值，由数据可知，虽然第3种起振电压较高，但是在振荡时，波形的高低电压差明显大于前两者，振荡效果好，尤其是在3V工作电压下更为显著，而且不需增加外部电容和内部限流电阻，大大节省了芯片面积，提高了性能。所以本设计采用第3种方案。

陶瓷谐振电路的暂态分析

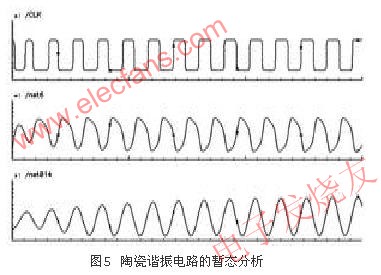
将陶瓷谐振器用图1中的等效电路代替，Cs为2pF，R为100?，L为18mH，C为16pF，振荡频率为455kHz。把陶瓷谐振器的等效电路并接在图4中的OSCI和OSCO上，CTRL端接高电平。采用南科公司的工艺库，在Cadence中进行Spectre仿真，波形图如图5所示。仿真时电源电压为3V。其中net014为振荡反相器的输入波形，net6(OSCO)为振荡反相器的输出波形，CLK为经过输出反相器的最终数字时钟。从仿真波形来看，开始的时候电路起振很快，振荡很快趋于稳定，CLK输出为455kHz的时钟信号。





交流频谱分析

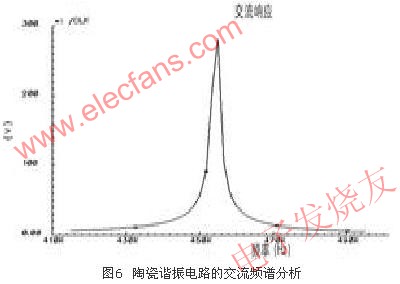
在Cadence的Analog Enviroment中做交流分析，结果如图6所示。由图可知，在455kHz左右时电路能量最大，小于或者低于此频率时，能量迅速衰减，由此更确定了此电路可以在455kHz下振荡的频谱特性。

结语

虽然陶瓷谐振电路结构简单，但是在集成时，尤其是将外接电容都集成在芯片内部时(本设计内部集成的电容共36pF，而一般公司做成的芯片都需要在OSCI和OSCO分别外接100pF电容)，需要恰当选择每个参数，才可以在最小的面积下实现最稳定的电路。本设计就是从这些角度出发，以实际流片测试作为主要手段，计算机为辅助，对每个参数进行了分析和确定，找到了在具体工艺下各参数值的最佳组合。