数字升压型功率因数校正转换器的分析与设计
时间:11-17
来源:互联网
点击:
摘要:本文以升压型转换器为AC-DC功率因数校正整流器的基本结构,控制核心采用DsPIC30F4011数字信号处理器,利用主动式功率因数校正技术的平均电流控制法,提高功率因数,减少输入电流谐波。为避免高功率因数转换器电压回路系统的带宽限制,额外加入负载电流以改善负载变动时输出电压的暂态响应。详细分析转换器、系统建模及控制器设计,开发一个450W的数字升压型功率因数校正转换器,通过试验验证转换器的高功率因数性能及输入电压幅值变动和负载变动时,输出电压的稳压性能。
传统AC/DC整流器因桥式整流器和滤波电容在整流过程中产生脉冲电流,造成低功率因数及电流谐波,需要对功率因数进行校正。理想的AC/DC转换器应具有两种特性:从电网端看须具备高功率因数的特性,从负载端看要有稳压性能。主动功率因数校正电路在运行校正电路连续导通模式(CCM)下,电路不具备功率因数校正的能力,需控制输入电流,使输入电流随输入电压波形及相位变化来提高功率因数[1-3]。利用平均电流控制的功率因数校正转换器对负载变动及输出电压的暂态响应较为迟缓,且需要复杂的控制电路及额外的乘/除器,数字电路等。而Figures[4]提出的负载电流法能有效改善输出电压暂态响应及稳压特性[5-6]。
本文以数字信号处理器DsPIC30F4011为基础,采用平均电流控制法与负载电流注入控制法实现数字控制高功率因数升压型AC/DC转换器系统。整个系统包括内回路电流控制、外回路电压控制及负载电流注入控制,通过该系统能在负载和输入电压幅值变动时,提高转换器的功率因数及输出电压的稳压性能。
1 升压型转换器系统
以数字信号处理器为基础的数字控制高功率因数转换器的系统结构如图1所示。其中内回路系统电流控制的作用是使输入电流随输入电压变化,以达到高功率因数性能;外回路电压控制作用是当输入电压幅值及负载变动时,整流器都能具有良好的输出稳压性能;负载电流注入控制的作用是将负载电流状态纳入反馈控制电路,以改善输出电压的暂态响应特性[7-8]。
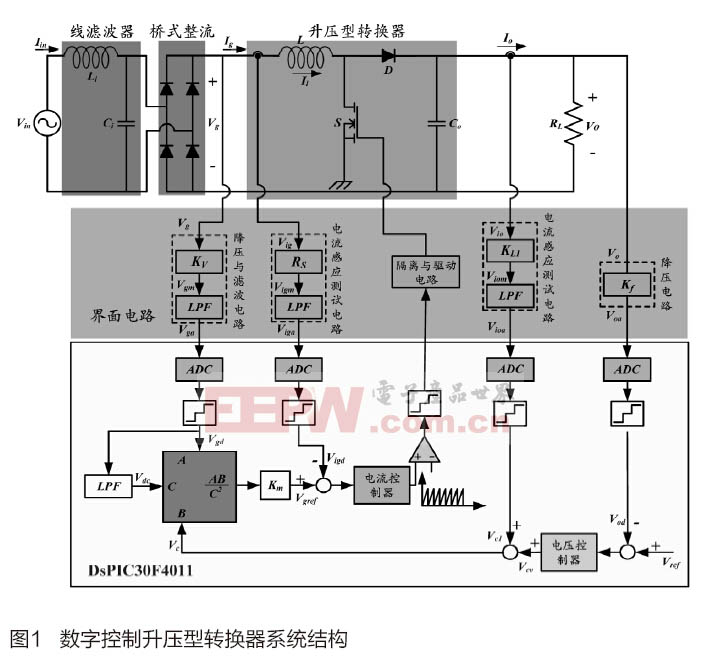
以平均电流控制法为基础的高功率因数升压型转换器的系统方框图如图2所示,为设计内回路电流控制器及外回路电路电压控制器,以提高系统功率因数及输出稳压性能,首先必须对升压型转换器进行分析,并建立受控系统模型,得出相应的数学模型,以此作为控制器设计基础。

2 高功率因数升压型转换器分析与建模
2.1 升压型转换器分析
高功率因数升压型转换器如图3所示,经过桥式整流的电压源

的全波波型,线电压半周期为

。在稳态分析前,假设:(1)切换周期Ts,开关导通比d;(2)电路运行在连续导通模式;(3)输出电容足够大,使输出电压为固定值V0。

在稳态下,利用伏秒平衡定理有:
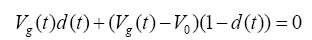
(1)
整理可得:
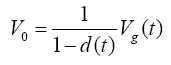
(2)
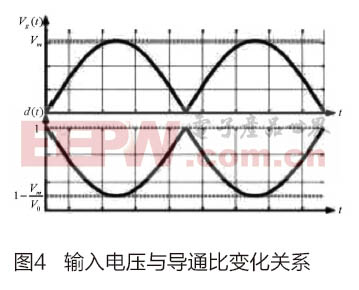
因为od(t)1,输出电压V0恒大于输入电压Vg。稳态时,输入电压与导通比变化关系如图4。
2.2 内回路电流控制系统建模
内回路电流控制的目的是让平均输入电流随输入电压波形变化,以达到高功率因数。通过对比感测电压Vidg与参考电压Viigref,得到误差信号ei,如图2所示。在经过电流控制器CI(S)和脉冲宽度调制器产生导通比d的驱动信号,控制开关的开和关,使平均输入电流随输入电压变化[9-10]。
为设计电流控制器,需建立控制系统的数学模型。本文利用状态空间平均法对升压型转换器作交流小信号分析,推导出控制系统的输出函数,作为CI(S)的设计基础。小信号分析可分为以下步骤:
1. 电路状态方程:升压型转换器如图3,若开关S打开,则二极管关闭,方程为:

(3)

(4)
若开关S关闭,则二极管打开,方程为:
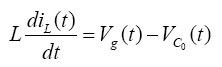
(5)
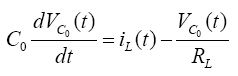
(6)
2. 线性化:对电感电流iL,输入电压Vg,电容电压Vc0,导通比d,忽略直流项及交流乘积项,可得线性方程式:
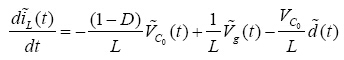
(7)
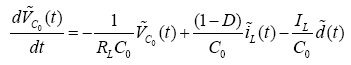
(8)
3. 传递函数:求出输出信号

对控制信号导通比

的传递函数为:

(9)
2.3 外回路电压控制系统建模
假设内回路电流控制器CI(S)设计合理,使平均输入电流随输入电压变化,利用平均功率法,对外回路电压控制系统的控制系统建模,求出传递函数,作为电压控制器的设计基础,以达到输出电压的稳压性能。如图2所示的功率因数校正转换器系统方框图,可得:

(10)
当
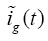
随Vg(t)变化,则
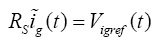
,
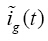
可表示为:
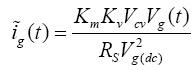
(11)
假设转换器转换效率为100%,即Pin(t)=P0(t),则平均输入功率为:
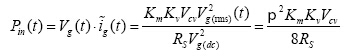
(12)
其中,Vg(t)的均方根值为Vg(nms) 与平均值为Vg(dc) 的比值为
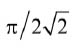
。因此,平均输出功率为:

(13)
因此可得:

(14)
根据理想高功率因数转换器的无损电阻器模式,如图5所示。对于线电压半周期T2L的移动平均值而言,控制信号发VCV与输入电压平均值Vg(dc) 的变化相当缓慢,可视为常数。

由式(12)和式(14)求得:
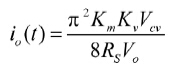
(15)
另一方面,因为
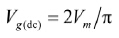
,所以:
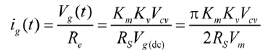
(16)
直流分析:由式(15)和(16)可得直流工作点
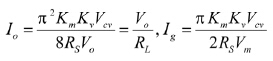
(17)
交流分析:忽略直流项与交流高次项,可得:

(18)
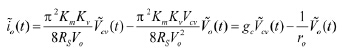
(19)
求得控制信号

至输出电压
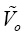
之间的传递函数为:
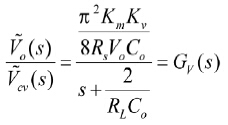
(20)
传统AC/DC整流器因桥式整流器和滤波电容在整流过程中产生脉冲电流,造成低功率因数及电流谐波,需要对功率因数进行校正。理想的AC/DC转换器应具有两种特性:从电网端看须具备高功率因数的特性,从负载端看要有稳压性能。主动功率因数校正电路在运行校正电路连续导通模式(CCM)下,电路不具备功率因数校正的能力,需控制输入电流,使输入电流随输入电压波形及相位变化来提高功率因数[1-3]。利用平均电流控制的功率因数校正转换器对负载变动及输出电压的暂态响应较为迟缓,且需要复杂的控制电路及额外的乘/除器,数字电路等。而Figures[4]提出的负载电流法能有效改善输出电压暂态响应及稳压特性[5-6]。
本文以数字信号处理器DsPIC30F4011为基础,采用平均电流控制法与负载电流注入控制法实现数字控制高功率因数升压型AC/DC转换器系统。整个系统包括内回路电流控制、外回路电压控制及负载电流注入控制,通过该系统能在负载和输入电压幅值变动时,提高转换器的功率因数及输出电压的稳压性能。
1 升压型转换器系统
以数字信号处理器为基础的数字控制高功率因数转换器的系统结构如图1所示。其中内回路系统电流控制的作用是使输入电流随输入电压变化,以达到高功率因数性能;外回路电压控制作用是当输入电压幅值及负载变动时,整流器都能具有良好的输出稳压性能;负载电流注入控制的作用是将负载电流状态纳入反馈控制电路,以改善输出电压的暂态响应特性[7-8]。

以平均电流控制法为基础的高功率因数升压型转换器的系统方框图如图2所示,为设计内回路电流控制器及外回路电路电压控制器,以提高系统功率因数及输出稳压性能,首先必须对升压型转换器进行分析,并建立受控系统模型,得出相应的数学模型,以此作为控制器设计基础。

2 高功率因数升压型转换器分析与建模
2.1 升压型转换器分析
高功率因数升压型转换器如图3所示,经过桥式整流的电压源

的全波波型,线电压半周期为

。在稳态分析前,假设:(1)切换周期Ts,开关导通比d;(2)电路运行在连续导通模式;(3)输出电容足够大,使输出电压为固定值V0。

在稳态下,利用伏秒平衡定理有:
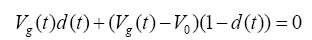
(1)
整理可得:
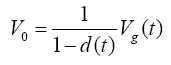
(2)
因为od(t)1,输出电压V0恒大于输入电压Vg。稳态时,输入电压与导通比变化关系如图4。

2.2 内回路电流控制系统建模
内回路电流控制的目的是让平均输入电流随输入电压波形变化,以达到高功率因数。通过对比感测电压Vidg与参考电压Viigref,得到误差信号ei,如图2所示。在经过电流控制器CI(S)和脉冲宽度调制器产生导通比d的驱动信号,控制开关的开和关,使平均输入电流随输入电压变化[9-10]。
为设计电流控制器,需建立控制系统的数学模型。本文利用状态空间平均法对升压型转换器作交流小信号分析,推导出控制系统的输出函数,作为CI(S)的设计基础。小信号分析可分为以下步骤:
1. 电路状态方程:升压型转换器如图3,若开关S打开,则二极管关闭,方程为:

(3)

(4)
若开关S关闭,则二极管打开,方程为:
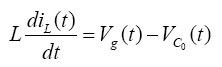
(5)
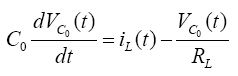
(6)
2. 线性化:对电感电流iL,输入电压Vg,电容电压Vc0,导通比d,忽略直流项及交流乘积项,可得线性方程式:
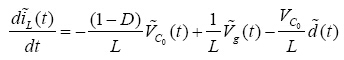
(7)
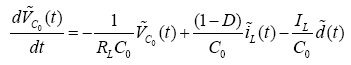
(8)
3. 传递函数:求出输出信号

对控制信号导通比

的传递函数为:

(9)
2.3 外回路电压控制系统建模
假设内回路电流控制器CI(S)设计合理,使平均输入电流随输入电压变化,利用平均功率法,对外回路电压控制系统的控制系统建模,求出传递函数,作为电压控制器的设计基础,以达到输出电压的稳压性能。如图2所示的功率因数校正转换器系统方框图,可得:

(10)
当
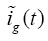
随Vg(t)变化,则
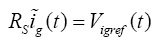
,
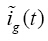
可表示为:
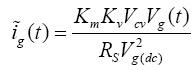
(11)
假设转换器转换效率为100%,即Pin(t)=P0(t),则平均输入功率为:
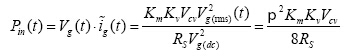
(12)
其中,Vg(t)的均方根值为Vg(nms) 与平均值为Vg(dc) 的比值为
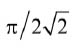
。因此,平均输出功率为:

(13)
因此可得:

(14)
根据理想高功率因数转换器的无损电阻器模式,如图5所示。对于线电压半周期T2L的移动平均值而言,控制信号发VCV与输入电压平均值Vg(dc) 的变化相当缓慢,可视为常数。

由式(12)和式(14)求得:
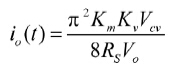
(15)
另一方面,因为
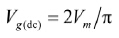
,所以:
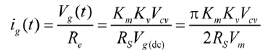
(16)
直流分析:由式(15)和(16)可得直流工作点
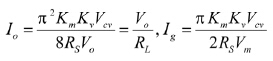
(17)
交流分析:忽略直流项与交流高次项,可得:

(18)
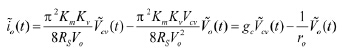
(19)
求得控制信号

至输出电压
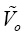
之间的传递函数为:
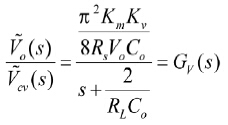
(20)
PIC 电流 电压 电容 电路 二极管 电感 电阻 万用表 开关电源 电子 相关文章:
- 电源设计小贴士 7:高效驱动 LED 离线式照明(04-05)
- DC-DC变换器中一种高性能振荡电路的设计(04-08)
- 使用低侧PWM IC的降压转换器(08-04)
- 多重转换:冗余电源系统电流限制的一种新方法(12-24)
- 对双向可控硅内部电路的探讨(05-18)
- 电流模式控制移相全桥零电压软开关(ZVS)DC/DC功率变换器(06-11)
