基于CMAC神经网络的PID参数自整定方法的研究
时间:12-07
来源:互联网
点击:
4 CMAC神经网络训练
CMAC神经网络的主要参数有:输入变量的量化精度、泛化参数以及基函数的种类。对CMAC神经网络的三个输入分别进行量化,阻尼比ζ分为23级,超调量百分比σ分为12个等级,衰减振荡周期Tc分为20个等级,共有23*12*20=5520种训练模式。
在所有5520种训练模式中选取2000种,作为CMAC参数整定网络的选练样本。再在2000组特征参数模式中选取1620组特征参数模式作为训练集对网络进行训练。
建立输入到物理存储空间的映射,同时建立了物理存储空间与输出的关系。泛化参数选为32,学习算法采用了误差纠正算法。学习率β为0.6,采用样条函数SPLINE替代传统的ALBUS函数作为CMAC神经网络的基函数。ALBUS函数的输出只有0和1,因此输出的曲线分段连续,仅在内节点之间连续,在内节点的分界处往往是不连续的。而样条函数则可以较好的解决这个问题。相应的内存使用量为300。
训练收敛后,权值体现了特征参数与PID控制器的待整定参数的关系。图4所示为CMAC神经网络对1620组特征参数模式的训练误差曲线。
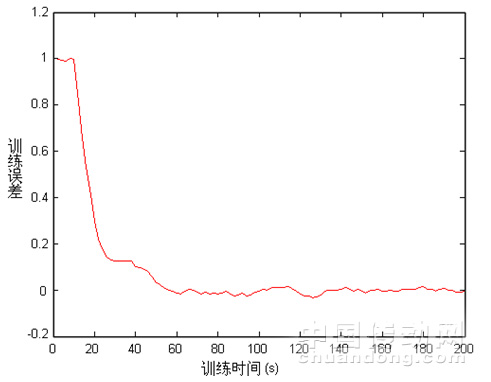
图4CMAC训练误差曲线
图5所示为1620组训练数据送入CMAC神经网络训练后,训练数据在各个误差区间中的个数,可看出超过90%的训练数据具有较高的误差精度,即误差精度<0.1。
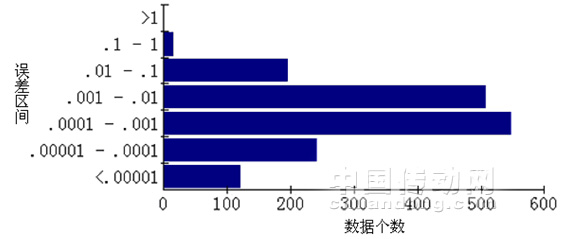
图5训练数据在各误差区间中的个数
把选取的2000种特征参数模块中剩下的380组作为测试集,对训练后的CMAC参数整定网络进行测试。输出的控制参数变化值与学习样本期望结果进行对比,错误率为7.8%,说明CMAC网络训练比较成功,具有一定的泛化能力。图6所示为CMAC神经网络的测试误差曲线。图7所示为测试数据在各误差区间中的个数。
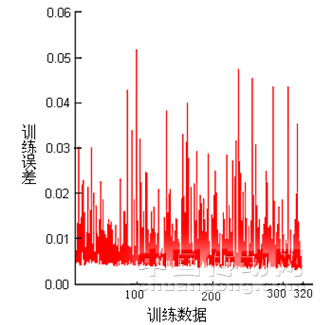
图6CMAC测试误差曲线
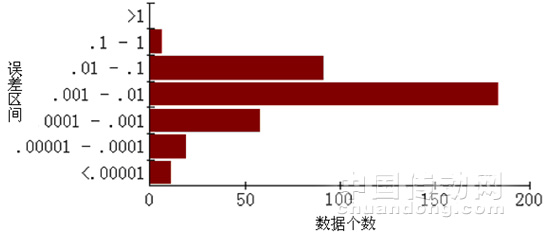
图7测试数据在各误差区间中的个数
5 仿真结果
选取被控对象为:
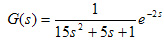
,原控制器对此对象的控制性能达到要求,阶跃扰动曲线如图8中线1所示。当进行PID参数自整定,整定后的响应曲线为图8中线2,把特征参量送入CMAC参数整定网络,整定后参数为
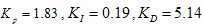
。从仿真图中,我们可以看出PID参数的整定效果比较理想,且CMAC神经网络的达到稳定的训练时间也比较短。
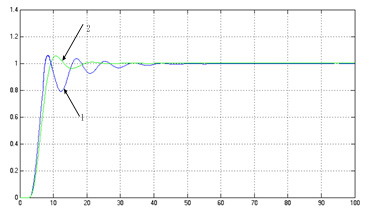
图8整定前后的响应曲线
6结论
仿真结果表明,CMAC神经网络的特性使其适合在PID参数自整定中使用。CMAC神经网络权值的调整是局部的,学习速度快,收敛性好,而且PID参数的整定效果也满足整定要求。文章的创新点:在基于模式识别的PID参数自整定系统中,直接利用CMAC网络获取整定规则,避免了传统的大量专家整定经验的建立。
CMAC神经网络的主要参数有:输入变量的量化精度、泛化参数以及基函数的种类。对CMAC神经网络的三个输入分别进行量化,阻尼比ζ分为23级,超调量百分比σ分为12个等级,衰减振荡周期Tc分为20个等级,共有23*12*20=5520种训练模式。
在所有5520种训练模式中选取2000种,作为CMAC参数整定网络的选练样本。再在2000组特征参数模式中选取1620组特征参数模式作为训练集对网络进行训练。
建立输入到物理存储空间的映射,同时建立了物理存储空间与输出的关系。泛化参数选为32,学习算法采用了误差纠正算法。学习率β为0.6,采用样条函数SPLINE替代传统的ALBUS函数作为CMAC神经网络的基函数。ALBUS函数的输出只有0和1,因此输出的曲线分段连续,仅在内节点之间连续,在内节点的分界处往往是不连续的。而样条函数则可以较好的解决这个问题。相应的内存使用量为300。
训练收敛后,权值体现了特征参数与PID控制器的待整定参数的关系。图4所示为CMAC神经网络对1620组特征参数模式的训练误差曲线。

图4CMAC训练误差曲线
图5所示为1620组训练数据送入CMAC神经网络训练后,训练数据在各个误差区间中的个数,可看出超过90%的训练数据具有较高的误差精度,即误差精度<0.1。

图5训练数据在各误差区间中的个数
把选取的2000种特征参数模块中剩下的380组作为测试集,对训练后的CMAC参数整定网络进行测试。输出的控制参数变化值与学习样本期望结果进行对比,错误率为7.8%,说明CMAC网络训练比较成功,具有一定的泛化能力。图6所示为CMAC神经网络的测试误差曲线。图7所示为测试数据在各误差区间中的个数。

图6CMAC测试误差曲线

图7测试数据在各误差区间中的个数
5 仿真结果
选取被控对象为:
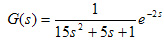
,原控制器对此对象的控制性能达到要求,阶跃扰动曲线如图8中线1所示。当进行PID参数自整定,整定后的响应曲线为图8中线2,把特征参量送入CMAC参数整定网络,整定后参数为
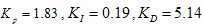
。从仿真图中,我们可以看出PID参数的整定效果比较理想,且CMAC神经网络的达到稳定的训练时间也比较短。

图8整定前后的响应曲线
6结论
仿真结果表明,CMAC神经网络的特性使其适合在PID参数自整定中使用。CMAC神经网络权值的调整是局部的,学习速度快,收敛性好,而且PID参数的整定效果也满足整定要求。文章的创新点:在基于模式识别的PID参数自整定系统中,直接利用CMAC网络获取整定规则,避免了传统的大量专家整定经验的建立。
- 基于音频信号的轴承故障诊断方法(03-17)
- 基于DSP的工业缝纫机控制系统设计(09-23)
- 智能门禁报警系统的仿真应用(10-20)
- 光电鼠标传感器的精密测量与控制系统(04-13)
- 基于双处理器的点焊控制系统的硬件设计(07-01)
- 凝气器污脏程度在线监测仪的研制(07-01)
