带Smith预估器的预测PID控制器的设计
时间:12-07
来源:互联网
点击:
3 仿真及分析
为仿真需要,考虑以下单变量模型:
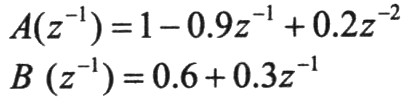
P=10,m=5,λ=1,B与k的值按仿真需要选取。
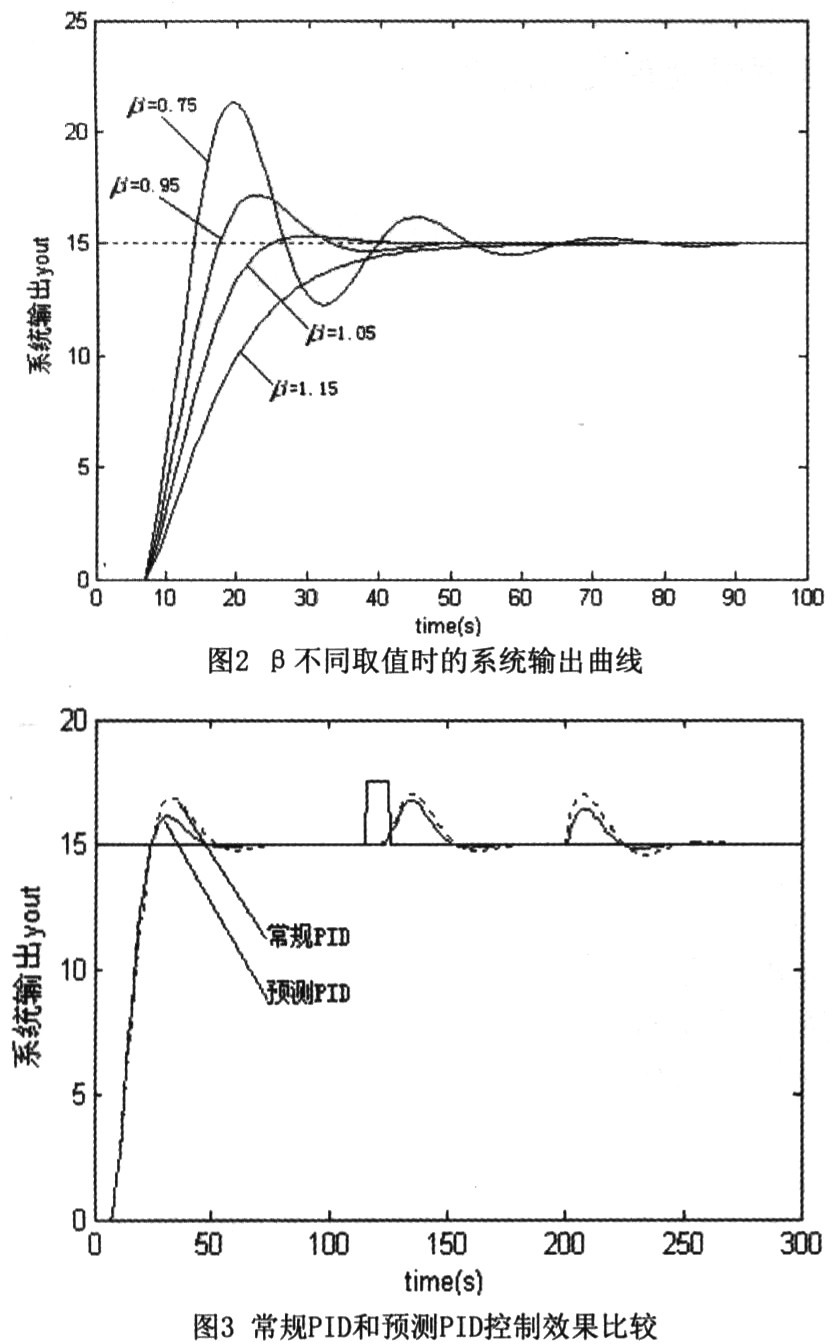
图2所示为K=7,β分别取0.75、0.95、1.05与1.15时,PID控制系统(无Smith补偿)的响应输出曲线,从图中可见,基于SGPC整定的PID控制器的动态性能可以很容易地通过选择不同的B值来调节,以获取合适的控制器参数,随着B取值的增加,系统的超调越小,响应速度则越慢,充分保持了SGPC控制的这一特点。
图3中,在110s处设定值发生幅值为20%、宽度为10s的脉冲扰动,以及在200s处,对象模型跃变为A1(z-1)=1-0.99z-1+0.25z-2,以及B1(z-1)=0.57+O.31z-1。从图中结果的对比可以看出,预测PID(β=0.95)比常规PID(Z-N法整定)控制器具有更好的动态响应特性,并且在出现外部扰动以及对象内部特性发生变化时体现出了更强的抗干扰性与鲁棒性。
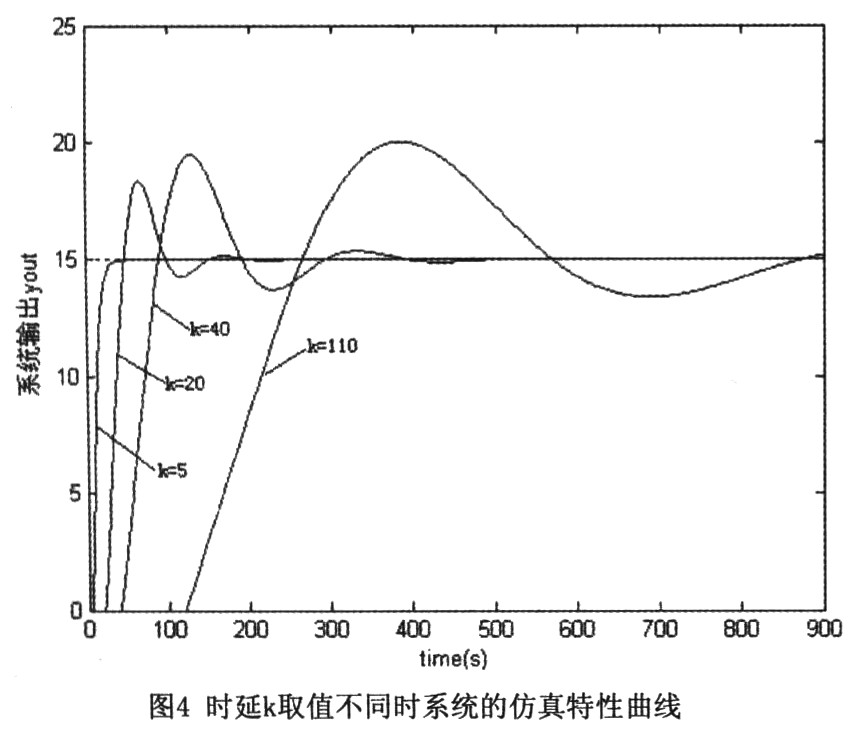
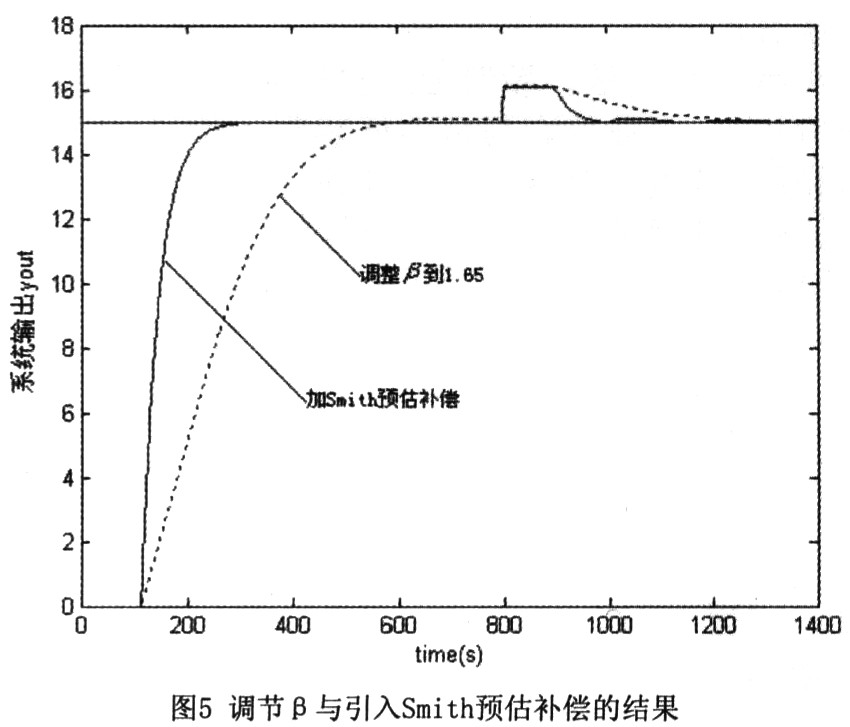
图4则是在其他参数保持不变(β=1.35),时延步数分别取值为5、20、40与110时,系统(无Smith补偿)的响应特性曲线,可以发现,随着时延的增加,系统的超调量及响应时间都有所增加,动态性能逐渐变差。由前文的分析可知,系统的动态响应性能可以通过改变β的大小来调节,另外在大时延系统中也可以通过引入Smith预估器来补偿时延,这里以k=110为例,对这两种方法进行比较,结果如图5所示(800s处模型跃变为A1(z-1),B1(z-1)以及时延k变为100)。很显然,增加B的值,虽然可以很好地改善系统的超调量,但却无法兼顾系统的响应时间,这对于那些对系统超调及响应时间都有要求的对象来说是不可取的,而加入Smith预估补偿的方法,则可以消除延时的影响,使大时延系统的超调量及响应速度都得到大大改善,并且很好地保持了系统的鲁棒性。
4 结论
文中讨论了基于SGPC的PID参数整定问题。仿真结果表明,此方法较常规PID具有更好的控制性能,而且自适应Smith预估器的引入可以克服大时延系统的整定误差,并且充分保持了系统的鲁棒性。本研究为工业过程控制中的大滞后、时变等复杂系统的控制提供了一种良好的选用方案。
为仿真需要,考虑以下单变量模型:
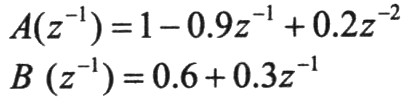
P=10,m=5,λ=1,B与k的值按仿真需要选取。

图2所示为K=7,β分别取0.75、0.95、1.05与1.15时,PID控制系统(无Smith补偿)的响应输出曲线,从图中可见,基于SGPC整定的PID控制器的动态性能可以很容易地通过选择不同的B值来调节,以获取合适的控制器参数,随着B取值的增加,系统的超调越小,响应速度则越慢,充分保持了SGPC控制的这一特点。
图3中,在110s处设定值发生幅值为20%、宽度为10s的脉冲扰动,以及在200s处,对象模型跃变为A1(z-1)=1-0.99z-1+0.25z-2,以及B1(z-1)=0.57+O.31z-1。从图中结果的对比可以看出,预测PID(β=0.95)比常规PID(Z-N法整定)控制器具有更好的动态响应特性,并且在出现外部扰动以及对象内部特性发生变化时体现出了更强的抗干扰性与鲁棒性。


图4则是在其他参数保持不变(β=1.35),时延步数分别取值为5、20、40与110时,系统(无Smith补偿)的响应特性曲线,可以发现,随着时延的增加,系统的超调量及响应时间都有所增加,动态性能逐渐变差。由前文的分析可知,系统的动态响应性能可以通过改变β的大小来调节,另外在大时延系统中也可以通过引入Smith预估器来补偿时延,这里以k=110为例,对这两种方法进行比较,结果如图5所示(800s处模型跃变为A1(z-1),B1(z-1)以及时延k变为100)。很显然,增加B的值,虽然可以很好地改善系统的超调量,但却无法兼顾系统的响应时间,这对于那些对系统超调及响应时间都有要求的对象来说是不可取的,而加入Smith预估补偿的方法,则可以消除延时的影响,使大时延系统的超调量及响应速度都得到大大改善,并且很好地保持了系统的鲁棒性。
4 结论
文中讨论了基于SGPC的PID参数整定问题。仿真结果表明,此方法较常规PID具有更好的控制性能,而且自适应Smith预估器的引入可以克服大时延系统的整定误差,并且充分保持了系统的鲁棒性。本研究为工业过程控制中的大滞后、时变等复杂系统的控制提供了一种良好的选用方案。
仿真 相关文章:
- ARM在数字化远程视频监控系统的应用(05-20)
- FPGA在弹上信息处理机中的应用(04-15)
- 与MSP430 USI端口配合使用ADS8361(06-18)
- 基于ARM的I2C设备控制方法的实现(06-11)
- 辰汉电子推出低成本快速量产视频监控方案+4路输入方案(06-24)
- 无线IP视频监控应用即将井喷,Blackfin助您赢得先机(07-23)
