带Smith预估器的预测PID控制器的设计
时间:12-07
来源:互联网
点击:
PID控制器因算法简单、鲁棒性好、可靠性高,一直是工业生产过程中应用最广的控制器。然而,实际生产过程往往具有非线性、时变不确定性,应用常规PID控制不能达到理想的控制效果。这时,往往不得不采用模型预测控制、自适应控制等先进控制策略来获得更好的控制性能。但是也存在多种原因阻碍这些先进控制策略在实际中的应用。其中一个主要的原因就是由于这类先进的控制算法在硬件、软件和人员培训方面缺乏有效的支持,这阻碍了它们在DCS层上的实现。而且在参数整定方面,由于这类算法的参数常缺乏明确的物理意义,对于已熟悉PID参数整定的操作人员来说,也是不得不面对的问题。因此,近年来越来越多的研究人员就上层采用模型预测控制这类先进的控制算法,而底层保留传统的PID控制算法,即所谓的预测PID控制算法,展开了一系列的研究。如P.Vega等人直接将经典PID的参数引入到性能指标中,再通过Taylor近似处理得到了次优化的控制器参数。Miller提出了一种随机预测PID控制算法,其在数学上等于稳态加权广义预测控制算法,并先后成功应于化肥厂热交换器的温度控制和废水装置溶氧浓度的控制。在文献中,MASARU KATAYAMA根据PID与一般GPC控制律之间的对应关系,直接计算出PID参数的值,本文在其基础上,采用阶梯式策略,避免了参数整定过程中复杂的矩阵求逆运算,并给控制输出引入较强的阶梯约束,改善了控制性能的调节灵活性。另外,文中分析了该方法在整定大延时对象的控制器参数时所引起的误差的原因,并通过引入smith预估器,有效地改善了这类系统的控制效果。
1 整定算法
1.1 系统描述及PID控制律介绍
考虑到GPC算法的需要,本文采用受控自回归积分滑动平均模型(CARIMA)描述被控对象:

其中,y(t)和u(t)为系统在t时刻的输出值和控制量;ζ(t)为零均值、方差有界的白噪声;k为系统的最小时延;△=1-z-1为差分算子;A(z-1)、B(z-1)分别为后移算子z-1的na和nb阶多项式,且A(z-1)为首一多项式。
文中控制器采用I-PD型结构,该控制律在改变设定值时,控制器输出不至于有太大的变化,增强了系统的抗扰动能力,另外可以很方便地得到此I-PD控制律与GPC控制律之间的联系,从而可以依据GPC思想来进行PID参数的整定。其具体形式为:
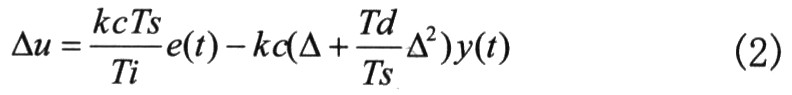
其中,e(t)=w(t)-y(t)为误差信号,w(t)为参考信号,kc、Ti、Td分别为比例增益、积分时问和微分时间,Ts为采样时间。对上式进行展开整理可得如下形式:

1.2 SGPC算法
按照GPC的一般理论,由模型(1)和Diophantine方程,得到t时刻对未来t+k+i(i=0,1,L,P-1)时刻系统输出的最优预测:

为最优预测中的自由响应部分,Fk+i(z-1)和Gk+i(z-1)是由Diophantine方程确定的z-1的多项式,
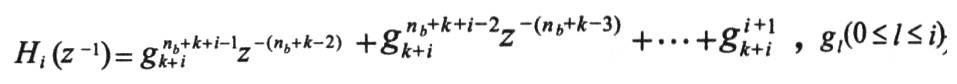
是对象阶跃响应的第l项系数,可以写成矩阵形式Y=Y1+G·△U,则实际的输出为Y=Y+E,E为误差向量。
GPC一般性能指标为
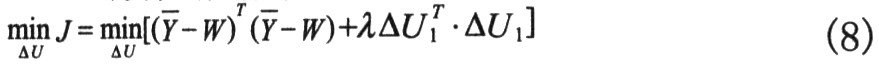
其中△U1=(△ut△ut+1…△ut+m-1),m为控制步长,λ为控制增量的权重。
由上述各式,根据传统的GPC算法,令J对△U1的偏导数为0,可以得到一个控制量序列[6,9],为简化计算,Diophantine方程一般用递推算法求解,但仍然不能避免矩阵求逆,计算量大,且不能保证矩阵可逆,计算中还会出现数值病态问题,在实际应用中存在着较大的安全隐患。
为避免传统GPC中的矩阵求逆问题,在算法中引入阶梯式策略。令

由Diophantine方程可知F(1)=Q,因此式(13)亦可表示为式(5)的形式,此时
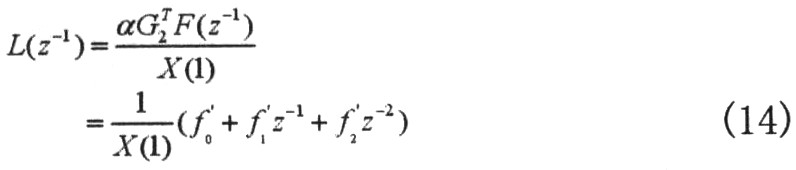
1.3 整定结果
由式(4)与式(14)的对应关系,我们可以比较得到PID控制器各参数(其中Ts为采样周期)如下:

2 整定算法的分析
2.1 参数调节的问题
本文通过引入阶梯因子,避免了参数整定过程中矩阵求逆,大大简化了计算。同时,在实际系统中,由于执行机构性能的限制,若控制量变化频率高,不仅执行机构动作跟不上,起不到作用,而且会增加执行机构的磨损。而阶梯式策略假定控制增量服从一个等比序列,这相当于给控制增量加了一个较强的限制。另外,由于引进阶梯因子后,加权因子λ性能的影响减小,而且其对于控制量的抵制作用也变得比较复杂,因此我们主要可以通过β来调节对应PID控制器的鲁棒性与快速性。
2.2 整定误差的Smith补偿
在前述的算法推导中,可以发现,为了建立I-PD与SGPC之间的相互联系,对多项式X(z-1)进行了静态处理,由式(12)与 式(13)可以看出,这样的处理,相当于认为过去k+nb-1步的输入变化量都相等,且等于当前时刻的输入变化量,即△ut-knb+1=△ut-k-nb+2=…=△ut,而实际运行中,在系统动态响应阶段,这种关系显然总是不成立的。这种近似处理,在系统无延时或小延时,即k取值很小时,影响可以忽略,但随着时延步数的加大,这种处理对系统鲁棒性地影响必将逐渐加剧,所以需要对具有大延时的系统进行补偿。因此,本文在系统中引入Smith预估器,以消除系统的时延影响,改善大延时系统的控制效果。
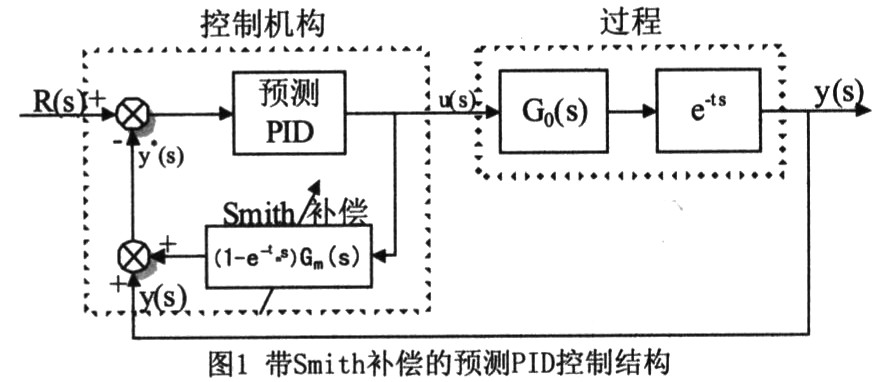
由于常规Smith预估器在模型失配时存在低鲁棒性问题,因此在应用中可采用文献中的自适应方案,即首先通过单变量寻优方法估计实际过程的纯滞后,然后再用带遗忘因子的最小二乘法辨识过程模型的其他参数,以在线修正模型。这样系统的控制结构可以设计成图1所示的形式。从图中可以看出,若系统无延时,系统等同于简单的预测PID控制回路,而当系统有时延时,延时对系统的影响即可由smith预估器消除,而预测PID参数则仅需根据无时延模型Gm(s)来整定,这样就可以避免时延带来的参数整定误差。
1 整定算法
1.1 系统描述及PID控制律介绍
考虑到GPC算法的需要,本文采用受控自回归积分滑动平均模型(CARIMA)描述被控对象:

其中,y(t)和u(t)为系统在t时刻的输出值和控制量;ζ(t)为零均值、方差有界的白噪声;k为系统的最小时延;△=1-z-1为差分算子;A(z-1)、B(z-1)分别为后移算子z-1的na和nb阶多项式,且A(z-1)为首一多项式。
文中控制器采用I-PD型结构,该控制律在改变设定值时,控制器输出不至于有太大的变化,增强了系统的抗扰动能力,另外可以很方便地得到此I-PD控制律与GPC控制律之间的联系,从而可以依据GPC思想来进行PID参数的整定。其具体形式为:
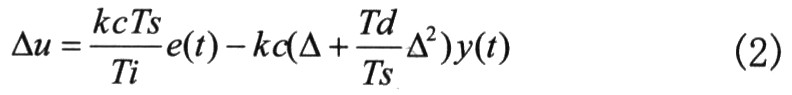
其中,e(t)=w(t)-y(t)为误差信号,w(t)为参考信号,kc、Ti、Td分别为比例增益、积分时问和微分时间,Ts为采样时间。对上式进行展开整理可得如下形式:

1.2 SGPC算法
按照GPC的一般理论,由模型(1)和Diophantine方程,得到t时刻对未来t+k+i(i=0,1,L,P-1)时刻系统输出的最优预测:

为最优预测中的自由响应部分,Fk+i(z-1)和Gk+i(z-1)是由Diophantine方程确定的z-1的多项式,
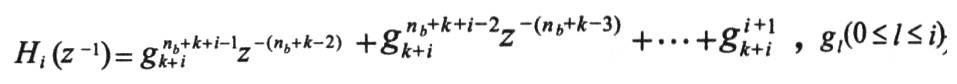
是对象阶跃响应的第l项系数,可以写成矩阵形式Y=Y1+G·△U,则实际的输出为Y=Y+E,E为误差向量。
GPC一般性能指标为
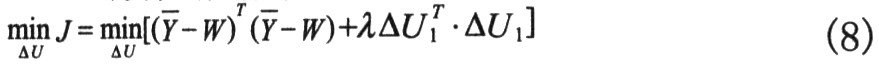
其中△U1=(△ut△ut+1…△ut+m-1),m为控制步长,λ为控制增量的权重。
由上述各式,根据传统的GPC算法,令J对△U1的偏导数为0,可以得到一个控制量序列[6,9],为简化计算,Diophantine方程一般用递推算法求解,但仍然不能避免矩阵求逆,计算量大,且不能保证矩阵可逆,计算中还会出现数值病态问题,在实际应用中存在着较大的安全隐患。
为避免传统GPC中的矩阵求逆问题,在算法中引入阶梯式策略。令

由Diophantine方程可知F(1)=Q,因此式(13)亦可表示为式(5)的形式,此时
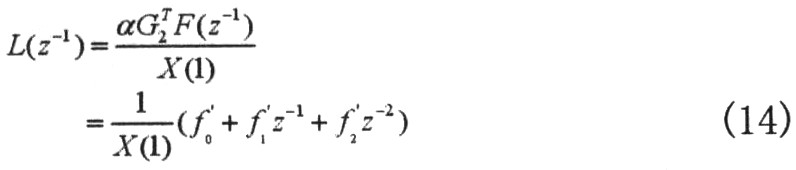
1.3 整定结果
由式(4)与式(14)的对应关系,我们可以比较得到PID控制器各参数(其中Ts为采样周期)如下:

2 整定算法的分析
2.1 参数调节的问题
本文通过引入阶梯因子,避免了参数整定过程中矩阵求逆,大大简化了计算。同时,在实际系统中,由于执行机构性能的限制,若控制量变化频率高,不仅执行机构动作跟不上,起不到作用,而且会增加执行机构的磨损。而阶梯式策略假定控制增量服从一个等比序列,这相当于给控制增量加了一个较强的限制。另外,由于引进阶梯因子后,加权因子λ性能的影响减小,而且其对于控制量的抵制作用也变得比较复杂,因此我们主要可以通过β来调节对应PID控制器的鲁棒性与快速性。
2.2 整定误差的Smith补偿
在前述的算法推导中,可以发现,为了建立I-PD与SGPC之间的相互联系,对多项式X(z-1)进行了静态处理,由式(12)与 式(13)可以看出,这样的处理,相当于认为过去k+nb-1步的输入变化量都相等,且等于当前时刻的输入变化量,即△ut-knb+1=△ut-k-nb+2=…=△ut,而实际运行中,在系统动态响应阶段,这种关系显然总是不成立的。这种近似处理,在系统无延时或小延时,即k取值很小时,影响可以忽略,但随着时延步数的加大,这种处理对系统鲁棒性地影响必将逐渐加剧,所以需要对具有大延时的系统进行补偿。因此,本文在系统中引入Smith预估器,以消除系统的时延影响,改善大延时系统的控制效果。

由于常规Smith预估器在模型失配时存在低鲁棒性问题,因此在应用中可采用文献中的自适应方案,即首先通过单变量寻优方法估计实际过程的纯滞后,然后再用带遗忘因子的最小二乘法辨识过程模型的其他参数,以在线修正模型。这样系统的控制结构可以设计成图1所示的形式。从图中可以看出,若系统无延时,系统等同于简单的预测PID控制回路,而当系统有时延时,延时对系统的影响即可由smith预估器消除,而预测PID参数则仅需根据无时延模型Gm(s)来整定,这样就可以避免时延带来的参数整定误差。
仿真 相关文章:
- ARM在数字化远程视频监控系统的应用(05-20)
- FPGA在弹上信息处理机中的应用(04-15)
- 与MSP430 USI端口配合使用ADS8361(06-18)
- 基于ARM的I2C设备控制方法的实现(06-11)
- 辰汉电子推出低成本快速量产视频监控方案+4路输入方案(06-24)
- 无线IP视频监控应用即将井喷,Blackfin助您赢得先机(07-23)
