基于DSP的两相无刷直流电机转速控制系统
时间:11-27
来源:互联网
点击:
稀土永磁无刷直流电机采用高性能的稀土永磁材料和非接触换相技术,体积小,效率高,无电火花,工作可靠,同时又具有类似普通直流电动机的调速性能,广泛应用于航空航天、精密仪器和工业控制自动化等领域。无刷直流电机采用电子换相装置,没有机械电刷;采用永磁体转子,没有激磁损耗;发热的电枢绕组置于外围的定子上,散热性好,效率高,过载能力强,无换相火花,在高转速领域尤为适合,是高速电机的一个重点发展方向。
目前,在一些特殊领域,对电机体积、连线数目以及可靠性等方面有着严格要求,在这些场合,无位置传感器无刷直流电机(BLDCM)就成了理想的选择。课题利用DSP,CPLD等数字化设计技术构建了一个体积较小的高转速、高可靠性电机转速控制系统。系统采用两相无刷直流电机,以无位置传感器方式,用电机绕组的反电势作为信号,由CPLD生成电机换相时序,通过硬件启动和锁相环跟踪,实现对无刷直流电机的稳速控制。该系统具有结构和电子控制线路简单、运行可靠、维护方便等特点。
1 无刷直流电机的数学模型
以两相导通、三相星形六状态为例,无刷直流电机三相绕组的电压平衡方程为:
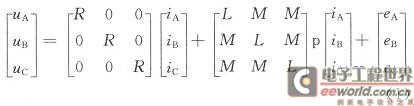
式中:uA,uB,uC为定子相绕组电压;eA,eB,eC为定子相绕组电动势;iA,iB,iC为定子相绕组电流;L为定子每相绕组自感;M为定子每两相绕组间的互感;R为三相定子电阻;p为微分算子。
由式(1)可以得到永磁无刷直流电动机的等效电路模型,如图l所示。

定子绕组产生的电磁转矩表达式为:

永磁无刷直流电机转子运动方程为:
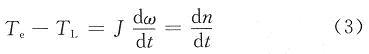
式中:Tn为电磁转矩;TL为负载转矩;B为阻尼系数;ω为电机机械转速;J为转动惯量。
2 控制系统的控制策略和硬件组成
2.1 控制系统的控制策略
系统采用转速、电流双闭环控制,用数字器件构成速度控制部分,电流环采用传统的PI调节器。DSP作为中央控制器,发出各种指令,并构成速度回路的PI调节器,可以进行智能PID控制; CPLD一部分构成锁相环用以检测输入频率与反馈频率的误差值,另一部分利用电枢反电势产生逆变器的换相控制信号。系统的控制原理框图如图2所示。
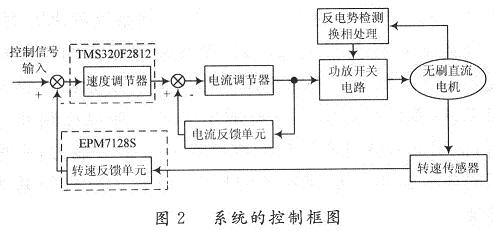
2.2 控制系统的硬件组成
无刷直流电机控制系统的硬件连接框图如图3所示,主要由无刷直流电机、逆变器、控制器和电源等组成。
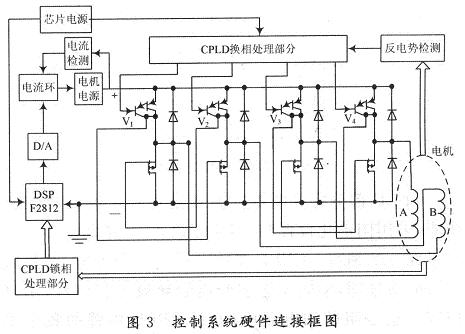
由于电机的转速较高,达到19 500 r/min,所以采用运算速度较快的大规模可编程逻辑器件(CPLD)进行速度反馈和电机换相信号的处理,TMS320F2812(DSP)构成速度控制器。电机的速度反馈量经CPLD的内置锁相环74LS297处理,产生偏差量输入DSP进行速度回路校正,经4通道、12位分辨率的D/A转换器 DAC7724输给电流控制器,经电流校正后进入逆变器,EPM7128S(CPLD)接收电机绕组的反电势产生控制4组功放开关的导通信号。电机有A, B两个绕组,两个绕组依次正、反导通,按照A-B-A-B的顺序连续给定子绕组通电,则转子就以一定的转速顺时针旋转。
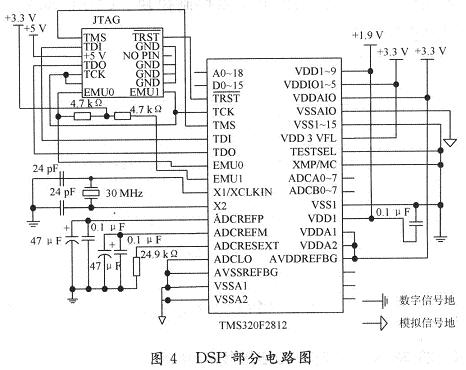
控制系统的DSP核心控制部分的硬件电路连接图如图4所示。
3 软件设计
系统软件由DSP程序和CPLD程序两部分组成。进行软件设计时,先进行系统分析,将整个程序按功能需求划分子模块。考虑到控制系统的实时性要求,采用中断方式编程,整个DSP软件系统由一个主程序和若干中断服务程序组成。
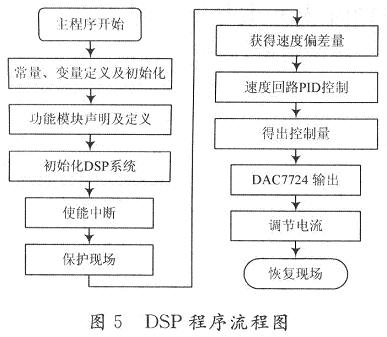
主程序的作用主要是对系统进行初始化,包括对DSP本身寄存器、中断、定时器、GPIO等进行初始化。初始化DSP,使其内部产生工作时钟;初始化DSP 内部模块;禁止全局中断,初始化中断向量表,根据需要对中断进行设置;打开全局中断,进入循环等待主程序,等待内部和外部中断信号。中断子程序完成转速环的校正控制任务。DSP中断子程序的流程图如图5所示。
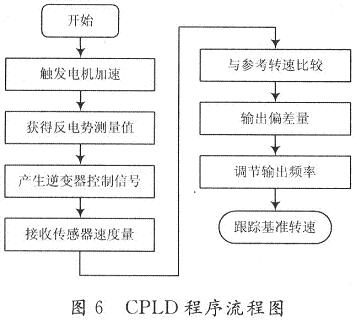
CPLD部分完成电机的换相处理和速度反馈控制功能,采用图形化设计和VHDL语言混合设计完成时序部分的编写。CPLD接收电机绕组反电势,经片内逻辑电路处理,形成4路逆变器的导通控制信号,用以控制电机绕组的加电顺序;通过CPLD内置的数字锁相环74LS297进行锁相处理,完成对电机转速的恒定控制。利用CPLD将锁相环和换相处理电路封装在一起,形成一个完整的速度反馈控制模块。CPLD部分程序流程图如图6所示。
4 控制系统仿真及其结果比较分析
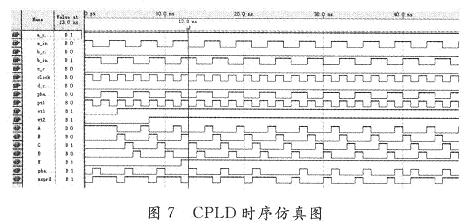
在进行了VHDL描述和编译后,就可应用EDA软件进行时序功能仿真。功能仿真是在QuartusⅡ软件开发环境下进行的,时序仿真波形如图7所示。
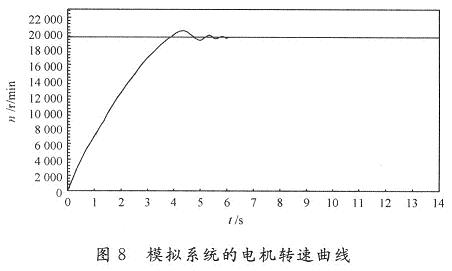
对速度控制器进行仿真,采用Matlab仿真软件进行,得到的模拟系统转速响应曲线如图8所示。
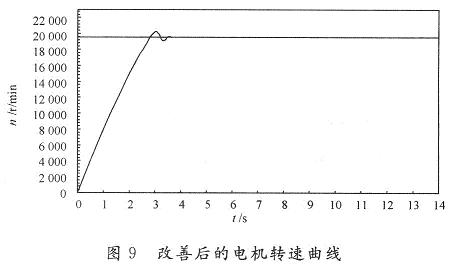
采用双线性变换法将连续系统离散化,得到的数字系统速度响应曲线如图9所示。
图中:n为电机转动速度;r为电机转数。
实验结果表明,改进后的数字系统的速度响应指标:上升时间、调节时间、超调量等均获得了改善,系统有着较好的快速性和稳定性。
目前,在一些特殊领域,对电机体积、连线数目以及可靠性等方面有着严格要求,在这些场合,无位置传感器无刷直流电机(BLDCM)就成了理想的选择。课题利用DSP,CPLD等数字化设计技术构建了一个体积较小的高转速、高可靠性电机转速控制系统。系统采用两相无刷直流电机,以无位置传感器方式,用电机绕组的反电势作为信号,由CPLD生成电机换相时序,通过硬件启动和锁相环跟踪,实现对无刷直流电机的稳速控制。该系统具有结构和电子控制线路简单、运行可靠、维护方便等特点。
1 无刷直流电机的数学模型
以两相导通、三相星形六状态为例,无刷直流电机三相绕组的电压平衡方程为:
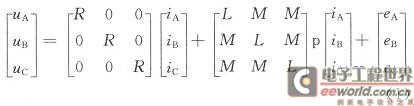
式中:uA,uB,uC为定子相绕组电压;eA,eB,eC为定子相绕组电动势;iA,iB,iC为定子相绕组电流;L为定子每相绕组自感;M为定子每两相绕组间的互感;R为三相定子电阻;p为微分算子。
由式(1)可以得到永磁无刷直流电动机的等效电路模型,如图l所示。

定子绕组产生的电磁转矩表达式为:

永磁无刷直流电机转子运动方程为:
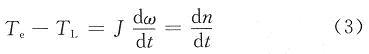
式中:Tn为电磁转矩;TL为负载转矩;B为阻尼系数;ω为电机机械转速;J为转动惯量。
2 控制系统的控制策略和硬件组成
2.1 控制系统的控制策略
系统采用转速、电流双闭环控制,用数字器件构成速度控制部分,电流环采用传统的PI调节器。DSP作为中央控制器,发出各种指令,并构成速度回路的PI调节器,可以进行智能PID控制; CPLD一部分构成锁相环用以检测输入频率与反馈频率的误差值,另一部分利用电枢反电势产生逆变器的换相控制信号。系统的控制原理框图如图2所示。

2.2 控制系统的硬件组成
无刷直流电机控制系统的硬件连接框图如图3所示,主要由无刷直流电机、逆变器、控制器和电源等组成。

由于电机的转速较高,达到19 500 r/min,所以采用运算速度较快的大规模可编程逻辑器件(CPLD)进行速度反馈和电机换相信号的处理,TMS320F2812(DSP)构成速度控制器。电机的速度反馈量经CPLD的内置锁相环74LS297处理,产生偏差量输入DSP进行速度回路校正,经4通道、12位分辨率的D/A转换器 DAC7724输给电流控制器,经电流校正后进入逆变器,EPM7128S(CPLD)接收电机绕组的反电势产生控制4组功放开关的导通信号。电机有A, B两个绕组,两个绕组依次正、反导通,按照A-B-A-B的顺序连续给定子绕组通电,则转子就以一定的转速顺时针旋转。
控制系统的DSP核心控制部分的硬件电路连接图如图4所示。

3 软件设计
系统软件由DSP程序和CPLD程序两部分组成。进行软件设计时,先进行系统分析,将整个程序按功能需求划分子模块。考虑到控制系统的实时性要求,采用中断方式编程,整个DSP软件系统由一个主程序和若干中断服务程序组成。
主程序的作用主要是对系统进行初始化,包括对DSP本身寄存器、中断、定时器、GPIO等进行初始化。初始化DSP,使其内部产生工作时钟;初始化DSP 内部模块;禁止全局中断,初始化中断向量表,根据需要对中断进行设置;打开全局中断,进入循环等待主程序,等待内部和外部中断信号。中断子程序完成转速环的校正控制任务。DSP中断子程序的流程图如图5所示。

CPLD部分完成电机的换相处理和速度反馈控制功能,采用图形化设计和VHDL语言混合设计完成时序部分的编写。CPLD接收电机绕组反电势,经片内逻辑电路处理,形成4路逆变器的导通控制信号,用以控制电机绕组的加电顺序;通过CPLD内置的数字锁相环74LS297进行锁相处理,完成对电机转速的恒定控制。利用CPLD将锁相环和换相处理电路封装在一起,形成一个完整的速度反馈控制模块。CPLD部分程序流程图如图6所示。

4 控制系统仿真及其结果比较分析
在进行了VHDL描述和编译后,就可应用EDA软件进行时序功能仿真。功能仿真是在QuartusⅡ软件开发环境下进行的,时序仿真波形如图7所示。

对速度控制器进行仿真,采用Matlab仿真软件进行,得到的模拟系统转速响应曲线如图8所示。

采用双线性变换法将连续系统离散化,得到的数字系统速度响应曲线如图9所示。

图中:n为电机转动速度;r为电机转数。
实验结果表明,改进后的数字系统的速度响应指标:上升时间、调节时间、超调量等均获得了改善,系统有着较好的快速性和稳定性。
电动机 自动化 电子 传感器 DSP CPLD 电压 电流 电阻 电路 逆变器 DAC VHDL 仿真 EDA Quartus 相关文章:
- 基于ARM微处理器LPC2132的智能电动机保护器设计(07-23)
- 基于ATmega8的大功率直流电机控制系统设计与实现(09-20)
- Atmega16在开关磁阻电机调速系统中的应用(06-08)
- DSP芯片介绍及其选型(06-07)
- 基于单片机AT89C51的时间/位移换向控制器设计(06-13)
- 单片机在电动机保护中的应用(07-23)
