采用DSP、PLD和ASIC实现多速滤波器设计的比较

许多通信系统都要用到多速滤波器(multirate filter)，多速滤波器是指输出数据速率与输入数据速率不相等的滤波器，常用于某个物理接口如数模转换器(DAC)或模数转换器(ADC)的接口处。当滤波器输出数据到DAC时，用户常会选择插值滤波器，因为它能产生更多的取样点以使DAC的输出波形更加平滑；而当滤波器从ADC接收信号时，用户一般会选用抽取滤波器，因为抽取滤波器允许数据被过取样从而获得更高的信噪比(SNR)。使用抽取滤波器后系统只需工作在信号速率。  

在多速滤波器设计过程中，有效地采用硬件实现插值和抽取功能非常重要，问题的关键还在于怎样选择正确的硬件类型。下面分别讨论采用DSP、PLD和ASIC实现多速滤波器的方法。  

插值和抽取  

插值功能常用来增加输出信号的取样率(图1)，实际上在原始取样值附近增加新的取样值很有必要。由于新的取样点处的值是未知数，一般就设为零，因此也被称为上取样(upsampling)、零值插入或零值填充。输出端数据点的增加会改变取样速率，从而使奈奎斯特频率外推。在时域中向数据插入零值，则信号在频域上会产生原始信号频谱的镜像。由于取样速率的改变并不会产生更多的信息，因此所有的镜像信号(以人工方式加入系统中)都表现为噪声，幸运的是这些噪声可以通过理想低通滤波器滤除。  



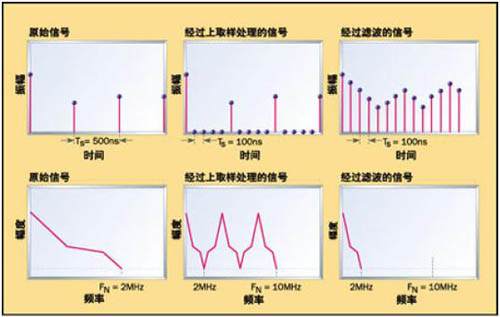
抽取滤波器的工作方式也大致相同。这种滤波器要消除某些取样点，从而降低取样速率和奈奎斯特频率。任何低于或高于奈奎斯特频率的信号都将表现为噪声，因此有必要在消除数据(下取样)前加入低通滤波器，这样可以确保噪声不串入系统(图2)。  



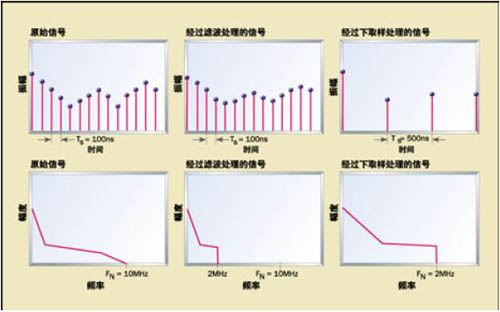
实现策略  

在插值与抽取实现方案中采用的低通滤波器最好具有线性相位特性，一般是利用有限冲击响应(FIR)滤波器来实现这种线性相位滤波器，但FIR滤波器的实现要比无限冲击响应滤波器(IIR)的代价高得多。为了取得更好的性能，需要增加滤波器的阶数，而FIR滤波器可以从10阶到200阶甚至更高。每个滤波器的输出必须经过10到200次运算。由于FIR滤波器非常昂贵，设计师一般会采用专用硬件来实现，这里的专用硬件可能是一块专用滤波芯片、一种可编程逻辑解决方案或一些半定制(标准化单元实现)集成电路。  

用标准单元实现的FIR滤波器可以获得最大的吞吐量，按速度排序的话，可编程逻辑器件(PLD)和专用滤波芯片的吞吐量排第二，然后才是通用DSP器件。当最终用户需要高的数据吞吐量时，几乎没有什么硬件可以胜过ASIC和PLD。ASIC设计流程相当成熟，对于PLD来说，可以利用能自动创建FIR滤波器的工具来加速开发流程。为了减小插值与抽取滤波器的芯片面积并增强其性能，很有必要采用一些专门技术。  

目前还没有最佳的多速滤波器实现方案，而方案的评估也有很多种方法。方案的成本取决于某个实现方案所对应的性能要求。这里性能可以定义为每秒钟乘法运算的总次数(由于加法一般都与乘法结合在一起，因此运算成本中不再包含加法)。假设单个乘法操作需要一个时钟周期，那么我们就可以确定实现某个方案所需的MIPS值。  

检查插值滤波器的运算速度有个比较直接的方法，即将数据先进行上取样然后再进行滤波。图3所示的样本要求采用388抽头的滤波器，并且滤波器工作时的数据速率必须达到每秒12兆样点(MSPS)。这种实现方式所要求的运算速率大约为4500MIPS。  



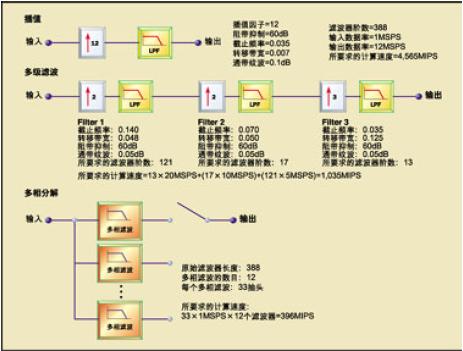
多级滤波  

好在有许多方法来降低运算速率要求，比如可以在三级内实现插值因子为12的多级滤波。设计人员可以将第一级的插值因子定为2，在第二级再以因子2对第一级的输出进行插值，然后输出到第三级，第三级的插值因子设为3，这样就有了3级滤波器，图3给出了每个滤波器的详细参数。  

通过分级插值可以降低对每个滤波器的要求，从而减少滤波器的阶数。另外，前二个滤波器分别工作在2MSPS和4MSPS，只有最后一个滤波器才工作在12MSPS，而改进前的方法要求整个滤波器工作在12MSPS。同样，若采用分级抽取，运算速率就不必要求太高。  

多级滤波法可以将运算速率减小到1035MIPS。对多级滤波器的各级重新分配运算任务，用小得多的滤波器就可以达到期望的运算结果，这是一种相对高水平的优化方法。

多相分解  

降低运算速率的另外一种方式需要详细分析插值滤波器的实现方案。众所周知，先进行零值插入然后滤波，就可以将问题分解到多个较短的滤波器中解决，每个滤波器工作于不同的时间点上，这种方法被称为多相分解，如图4所示。  



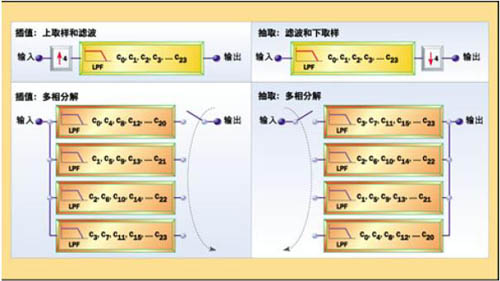
举个简单的例子来说明一下多相分解的工作原理。在该例中滤波器系数为24，插值因子为4。由于滤波器插值因子为4，因此实际上大多数输出到滤波器的数据为零，通过执行特殊的乘法操作可以消除这些零数据的系数。例如，第一个输出数据可以单独由系数C0、C4、C8……C20确定，而第二个输出数据则由C1、C5、C9……C21等系数决定。在这种情况下每个输出只要求6次乘法运算而不是24次乘法运算，调整插值因子可以减少运算速率。对于插值因子为12的388抽头滤波器，每个输出只需33次乘法即可确定。多相插值器可以用388MIPS完成相同的运算量。  

抽取结构同样也可利用类似的技术。在本例中抽取因子为4，因此4个数据点经过滤波后只剩下了1个，其实没有必要去计算被丢弃的取样点数。多相抽取器将数据分配给4个较短的多相滤波器(抽取因子为4)，最后将4个滤波器的输出叠加在一起从而形成最终滤波输出。每个多相滤波器以抽取后的数据速率输出数据，从而降低了对抽取器的性能要求。  

当然可以综合运用多种方法以进一步降低运算速率。例如，可以对多相结构中的每个单级滤波器执行多级滤波。