利用低功耗微控制器开发FFT应用

复数的极坐标转换

为了便于确定VIN频谱的幅度，我们须要将复数形式的X(k)转换为极坐标形式。实现该转换的固件示于程序清单5。幅度值取代了原始的FFT结果，因为固件不再需要这些数据。
清单5. FFT结果从复数形式转换为极坐标形式。  

const unsigned char magnLUT[16][16] =
{
{0x00,0x10,0x20, ... ,0xd0,0xe0,0xf0},
{0x10,0x16,0x23, ... ,0xd0,0xe0,0xf0},
...
{0xe0,0xe0,0xe2, ... ,0xff,0xff,0xff},
{0xf0,0xf0,0xf2, ... ,0xff,0xff,0xff}
};
...
...
/* Compute x_n_re=abs(x_n_re) and x_n_im=abs(x_n_im) */
...
...
x_n_re[0] = magnLUT[x_n_re[0]＞＞11][0];

for(i=1; i<n_div_2; i++)
x_n_re[ i] = magnLUT[x_n_re[ i]＞＞11][x_n_im[ i]＞＞11];

x_n_re[N_div_2] = magnLUT[x_n_re[N_div_2]＞＞11][0];

频谱幅度并非根据式4计算得到，而是通过一个二维LUT查表得到。第一索引为频谱实部的高4位(MSB)，第二索引为频谱虚部的高4位。为得到这些数据，可将带符号的16位数据右移11次。在从频谱的实部和虚部取得索引号前，需首先将它们转换为绝对值。因此，符号位为零。

从式6我们已经知道，频谱的幅度是关于X(N / 2)对称的，因此我们只需将前(N / 2) + 1个频谱数据转换为极坐标形式。还有，我们可以看到，对于实数输入采样，X(0)和X(N / 2)的虚部总为零。因此这两条谱线的幅度被单独计算。本项目实际固件的注释中包含了用于自动生成该LUT的源代码，可由程序调用来计算X(k)的幅度。

Hamming或Hann窗

此项目固件还包括了对输入采样加Hamming或Hann窗的LUT (Q8.7格式)。加窗函数可有效降低对时域采样x(n)的舍入操作所引起的频谱泄漏。Hamming和Hann窗函数分别如式7和8所示。



程序清单6给出了实现这些函数的代码。同样，本项目实际固件的注释中包含了用于自动生成这些LUT的源代码，可由程序调用来实现这些窗函数。

清单6. 用来实现Hamming和Hann窗函数的LUT。  

const char hammingLUT[N] = {+10, +10, +10, ... ,+10, +10, +10};
const char hannLUT[N] = { +0, +0, +0, ... , +0, +0, +0};
...
...
for(i=0; i＜256; i++)
{
#ifdef WINDOWING_HAMMING
MUL_1(x_n_re[ i],hammingLUT[ i],x_n_re[ i]); // x(n)*=hamming(n);
#endif
#ifdef WINDOWING_HANN
MUL_1(x_n_re[ i],hannLUT[ i]),x_n_re[ i]); // x(n)*=hann(n);
#endif
}

测试结果

为了测试该FFT应用的性能，固件将X(k)幅度通过μC的UART端口上传给PC。专门编写的FFT Graph软件(随该项目固件一起提供)用于从PC串口读取这些幅值，并以图形方式实时显示频谱。图3显示了μC以200ksps采样四种不同输入信号并处理后，由FFT Graph所显示出来的结果：

4.3V直流信号
50kHz正弦信号
70kHz正弦信号
6.25kHz方波  



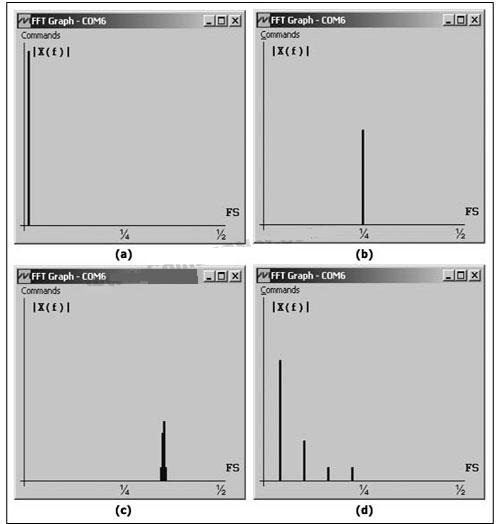
图3. FFT Graph软件显示的由低功耗μC计算出的频谱。  

接下来干什么？

有兴趣的读者还可以花费大量的时间来继续优化和重新配置该FFT应用。尽管在本文中我们选择了radix-2算法，还有很多其他算法可以显著降低加法和乘法运算量。很多本文所未提及的优化可以提升FFT的速度。例如，作为纯实数的输入采样，其虚部总为零，频谱中只有前半部分有实际意义。利用这一点，第一级和最后一级FFT的执行速度可进一步优化，但需要付出更多的程序空间。

总之，本文所讨论的算法对于低功耗μC上的FFT应用而言，提供了一个很好的出发点。如果想了解更多信息和具体实现的细节，请查阅我们为本应用所提供的、带有详细注释的固件信息。