利用低功耗微控制器开发FFT应用
时间:09-03
来源:互联网
点击:
今天的低功耗微控制器(μC)也开始集成原先只存在于大型微处理器、ASIC和DSP中的外设功能,使我们有可能以很低的功耗实现复杂的算术运算。本文讨论一种快速傅立叶变换(FFT)应用,并在一个含有单周期硬件乘法器的低功耗μC上实现该应用。
这个FFT应用实时计算一路输入电压(图1中的VIN)的频谱。为完成该任务,用一片模数转换器(ADC)对VIN进行采样,获得的采样传送给μC。然后,μC对这些采样执行256点FFT运算,获得输入电压的频谱。为便于检测,μC将计算出的频谱数据传送给PC,由PC实时显示出来。
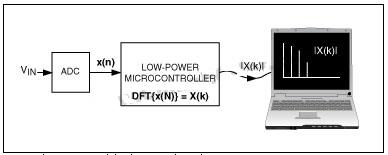
图1. 利用FFT应用计算输入电压的频谱。
该FFT应用的固件针对MAXQ2000系列中的一款16位、低功耗μC用C语言编写。有兴趣的读者可以下载(ZIP,2.4kb)该项目的固件和电路原理图。
背景知识
为确定输入信号采样的频谱,我们需要对这些输入采样进行离散傅立叶变换(DFT)。DFT的定义如下:

其中N是采样的数量,X(k)是频谱,x(n)是一组输入采样。利用欧拉等式展开求和符,并分离输入采样和频谱的实部和虚部,得到以下等式:
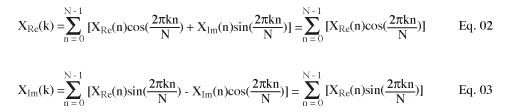
式2和3中,求和符中第二项的消失是由于输入采样全部为实数。假定我们有N个采样,直接计算式2和3需要2N2次乘法和2N(N - 1)次加法。这样,我们的256点输入采样DFT将需要进行131,072次乘法和130,560次加法运算。我们还是将注意力转向FFT吧!
有多种FFT算法可供使用。本应用采用普通的radix-2算法,继续将DFT分解为两个更小的DFT。为此,N必须是2的指数。这种radix-2 FFT算法的步骤可归纳如图2所示的蝶型运算。观察这些蝶型运算我们可以发现,radix-2算法仅需(N / 2)log2(N)次乘法和Nlog2(N)次加法。图2中用到的参数WN就是通常所谓的“旋转因子”,可以在执行算法前预先计算出来。
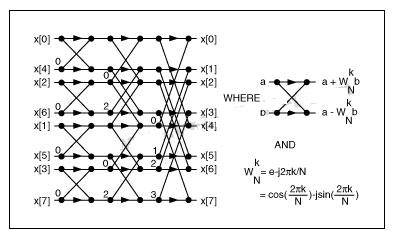
图2. 利用蝶型运算实现N = 8的FFT。
在图2中,FFT的输入显示为一种特殊的排列顺序,这种序列是对原始序列索引号的二进制位反转后得到的。因此,当我们对N = 8个采样执行radix-2 FFT算法时,需要将输入数据的原始序列:
0 (000b), 1 (001b), 2 (010b), 3 (011b), 4 (100b), 5(101b), 6(110b), 7(111b)
重新排列为:
0 (000b), 4, (100b), 2 (010b), 6 (110b), 1 (001b), 5 (101), 3 (011), 7 (111)
FFT输出则以正确的顺序排列。图2还说明,每个单独的蝶型运算所得的结果,是下一级FFT运算所需的唯一数据。由于运算过程可“即位”进行,新值可替代旧值,这样,计算N个采样的FFT只需要2N个变量(因为每个数据都包括实部和虚部两部分)。
& nbsp; FFT完成后,结果为复数形式。式4和5将结果转换为极坐标方式后表示为:

有关DSP的文献中可以找到很多优化方法,可使上述DFT/FFT算法更小或更快。其中最重要的一种优化方法(可能也是最容易实现的)源于这样一个事实,那就是作为一个实数信号,其DFT幅度是相关于X(N / 2)对称的,因此:

编写FFT代码绝非易事。低功耗μC的一些局限又进一步使该任务复杂化。
存储器:我们所选的μC有2kB的RAM。已经知道该算法需要用到2N个16位变量来存储FFT数据,这样,我们的μC可以执行N最高为512的FFT。然而,固件的其他部分也要用到一些RAM。因此,在此项目中,我们限制N于256。若采用16位变量来表示每个值的实部和虚部,FFT数据总共需要1024字节的RAM。
速度:低功耗μC尽管具有高MIPS/mA性能,仍然需要一些优化手段来使运行FFT的指令数尽可能少。好在本应用所用的C编译器(IAR的Embedded Workbench for MAXQ,见www.iar.com)可提供多种级别的优化和设置。高效地使用硬件乘法器可使代码优化到可以接受的水平。
无浮点能力:所选的μC不具备浮点能力(低功耗产品一般都不具备浮点能力)。因此,所有运算都必须采用定点算法。为了表示小数,固件采用带符号的Q8.7表示法。这样,在固件中假定:
第0位至第6位代表小数部分
第7位至第14位代表整数部分
第15位代表符号位(二的补码)
这样的安排对于加法和减法没有影响,但在做乘法时必须注意将数据按照Q8.7格式对齐。

所选的数据表示法还要适应FFT算法可能遇到的最大数值,同时又要提供足够的精度。例如,我们的ADC可提供带符号的8位采样,以二的补码表示。如果输入为最大幅度(对于带符号8位采样为127)的直流电压,则其能谱全部包含于X(0)中,用Q8.7表示为32512。这个数值能够由单个带符号的16位数据表示。
固件
以下部分讨论在低功耗μC上执行radix-2 FFT的固件实现。信号采样由ADC读出后被存储在x_n_re数组中。这个数组代表x(n)的实部。虚部存储在x_n_im数组中,在开始运行FFT前初始化为零。完成FFT后,计算结果取代原始采样数据,被存储在x_n_re和x_n_im中。
这个FFT应用实时计算一路输入电压(图1中的VIN)的频谱。为完成该任务,用一片模数转换器(ADC)对VIN进行采样,获得的采样传送给μC。然后,μC对这些采样执行256点FFT运算,获得输入电压的频谱。为便于检测,μC将计算出的频谱数据传送给PC,由PC实时显示出来。

图1. 利用FFT应用计算输入电压的频谱。
该FFT应用的固件针对MAXQ2000系列中的一款16位、低功耗μC用C语言编写。有兴趣的读者可以下载(ZIP,2.4kb)该项目的固件和电路原理图。
背景知识
为确定输入信号采样的频谱,我们需要对这些输入采样进行离散傅立叶变换(DFT)。DFT的定义如下:

其中N是采样的数量,X(k)是频谱,x(n)是一组输入采样。利用欧拉等式展开求和符,并分离输入采样和频谱的实部和虚部,得到以下等式:
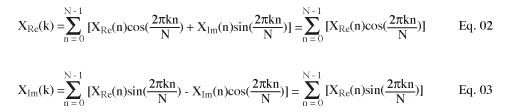
式2和3中,求和符中第二项的消失是由于输入采样全部为实数。假定我们有N个采样,直接计算式2和3需要2N2次乘法和2N(N - 1)次加法。这样,我们的256点输入采样DFT将需要进行131,072次乘法和130,560次加法运算。我们还是将注意力转向FFT吧!
有多种FFT算法可供使用。本应用采用普通的radix-2算法,继续将DFT分解为两个更小的DFT。为此,N必须是2的指数。这种radix-2 FFT算法的步骤可归纳如图2所示的蝶型运算。观察这些蝶型运算我们可以发现,radix-2算法仅需(N / 2)log2(N)次乘法和Nlog2(N)次加法。图2中用到的参数WN就是通常所谓的“旋转因子”,可以在执行算法前预先计算出来。

图2. 利用蝶型运算实现N = 8的FFT。
在图2中,FFT的输入显示为一种特殊的排列顺序,这种序列是对原始序列索引号的二进制位反转后得到的。因此,当我们对N = 8个采样执行radix-2 FFT算法时,需要将输入数据的原始序列:
0 (000b), 1 (001b), 2 (010b), 3 (011b), 4 (100b), 5(101b), 6(110b), 7(111b)
重新排列为:
0 (000b), 4, (100b), 2 (010b), 6 (110b), 1 (001b), 5 (101), 3 (011), 7 (111)
FFT输出则以正确的顺序排列。图2还说明,每个单独的蝶型运算所得的结果,是下一级FFT运算所需的唯一数据。由于运算过程可“即位”进行,新值可替代旧值,这样,计算N个采样的FFT只需要2N个变量(因为每个数据都包括实部和虚部两部分)。
& nbsp; FFT完成后,结果为复数形式。式4和5将结果转换为极坐标方式后表示为:

有关DSP的文献中可以找到很多优化方法,可使上述DFT/FFT算法更小或更快。其中最重要的一种优化方法(可能也是最容易实现的)源于这样一个事实,那就是作为一个实数信号,其DFT幅度是相关于X(N / 2)对称的,因此:

编写FFT代码绝非易事。低功耗μC的一些局限又进一步使该任务复杂化。
存储器:我们所选的μC有2kB的RAM。已经知道该算法需要用到2N个16位变量来存储FFT数据,这样,我们的μC可以执行N最高为512的FFT。然而,固件的其他部分也要用到一些RAM。因此,在此项目中,我们限制N于256。若采用16位变量来表示每个值的实部和虚部,FFT数据总共需要1024字节的RAM。
速度:低功耗μC尽管具有高MIPS/mA性能,仍然需要一些优化手段来使运行FFT的指令数尽可能少。好在本应用所用的C编译器(IAR的Embedded Workbench for MAXQ,见www.iar.com)可提供多种级别的优化和设置。高效地使用硬件乘法器可使代码优化到可以接受的水平。
无浮点能力:所选的μC不具备浮点能力(低功耗产品一般都不具备浮点能力)。因此,所有运算都必须采用定点算法。为了表示小数,固件采用带符号的Q8.7表示法。这样,在固件中假定:
第0位至第6位代表小数部分
第7位至第14位代表整数部分
第15位代表符号位(二的补码)
这样的安排对于加法和减法没有影响,但在做乘法时必须注意将数据按照Q8.7格式对齐。

所选的数据表示法还要适应FFT算法可能遇到的最大数值,同时又要提供足够的精度。例如,我们的ADC可提供带符号的8位采样,以二的补码表示。如果输入为最大幅度(对于带符号8位采样为127)的直流电压,则其能谱全部包含于X(0)中,用Q8.7表示为32512。这个数值能够由单个带符号的16位数据表示。
固件
以下部分讨论在低功耗μC上执行radix-2 FFT的固件实现。信号采样由ADC读出后被存储在x_n_re数组中。这个数组代表x(n)的实部。虚部存储在x_n_im数组中,在开始运行FFT前初始化为零。完成FFT后,计算结果取代原始采样数据,被存储在x_n_re和x_n_im中。
- F1aSh存储器在TMS320C3X系统中的应用(11-11)
- 基于PIC18F系列单片机的嵌入式系统设计(11-19)
- DSP在卫星测控多波束系统中的应用(01-25)
- 基于PCI总线的双DSP系统及WDM驱动程序设计(01-26)
- 利用Virtex-5 FPGA实现更高性能的方法(03-08)
- DSP与单片机通信的多种方案设计(03-08)
