SUSAN边缘检测算法性能分析与比较
时间:07-20
来源:互联网
点击:
1 引 言
边缘是图像最基本的特征,是图像分割的第一步。经典的边缘检测方法如:Roberts,Sobel,Prewitt,Kirsch,Laplace等方法,基本都是对原始图像中象素的小邻域构造边缘检测算子,进行一阶微分或二阶微分运算,求得梯度最大值或二阶导数的过零点,最后选取适当的阀值提取边界。由于这些算法涉及梯度的运算,因此均存在对噪声敏感、计算量大等缺点。在实践中,发现SUSAN算法只基于对周边象素的灰度比较,完全不涉及梯度的运算,因此其抗噪声能力很强,运算量也比较小。并将SUSAN算法用于多类图像的边缘检测中,实验证明该算法非常适合含噪图像的边缘检测。
2 SUSAN边缘检测简介
2.1 SUSAN特征检测原理
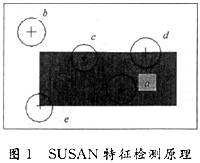
如图1所示,用一个圆形模板在图像上移动,若模板内象素的灰度与模板中心象素(称为:核Nucleus)灰度的差值小于一定阀值,则认为该点与核具有相同(或相近)的灰度,由满足这样条件的象素组成的区域称为USAN(Univalue Segment Assimilating Nucleus)。
当圆形模板完全处在图像或背景中时,USAN区域面积最大(如图1中的a和b);当模板移向图像边缘时,USAN区域逐渐变小(如图1中c);当模板中心处于边缘时,USAN区域很小(如图1中的d);当模板中心处于角点时,USAN区域最小(如图1中的e)。可以看出,在边缘处象素的USAN值都小于或等于其最大值的一半。因此,计算图像中每一个象素的USAN值,通过设定一个USAN阀值,查找小于阀值的象素点,即可确定为边缘点[1]。
2.2 SUSAN边缘检测算法
(1)算法描述
对整幅图像中的所有象素,用圆形模板进行扫描,比较模板内每一象素与中心象素的灰度值,通过与给定的阀值比较,来判别该象素是否属于USAN区域,如下式:
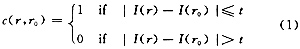
式(1)中c(r,r0)为模板内属于USAN区域的象素的判别函数;I(r0)是模板中心象素(核)的灰度值;I(r)为模板内其他任意象素的灰度值;t是灰度差门限。
图像中每一点的USAN区域大小可用下式表示:
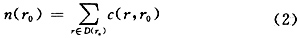
式(2)中D(r0)为以r0为中心的圆形模板区域。得到每个象素的USAN值n(r0)以后,再与预先设定得门限g进行比较,当n(r0)<g时,所检测到象素位置r0可以认为是一个边缘点。
(2)模板的选取
由于图像的数字化,实际上无法实现真正的圆形模板,所以都是采用近似圆代替。但是模板较小时,如果门限选取不恰当,可能会发生边缘点漏检的情况。模板也不宜取得太大,否则会增大运算量大,通常可取5×5或37象素模板[1]。本文实验中均采用的是5×5的模板。
(3)门限t,g的确定
门限g决定了边缘点的USAN区域的最大值,即只要图像中的象素的USAN值小于g,该点就被判定为边缘点。g过大时,边缘点附近的象素可能作为边缘被提取出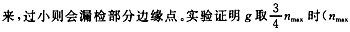 为模板的最大USAN值),可以较好地提取出初始边缘点。如果要达到单象素的精度,还需进一步剔除多余象素。
为模板的最大USAN值),可以较好地提取出初始边缘点。如果要达到单象素的精度,还需进一步剔除多余象素。
门限t表示所能检测边缘点的最小对比度,也是能忽略的噪声的最大容限。t越小,可从对比度越低的图像中提取特征。因此对于不同对比度和噪声情况的图像,应取不同的t值[2]。
3 实 验
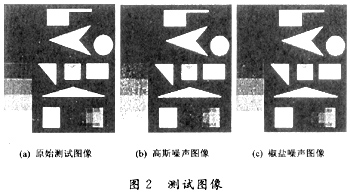
在主频2.3 GHz,内存256 MB的PC机上,分别对SUSAN算法(t=10,g=18)和传统的Robert算子、Gauss-Laplace算子、Prewitt算子,采用Visal C++编程,对图2中的3幅灰度测试图像进行边缘检测。图2中(a)是原始测试图像,(b)是加入高斯噪声(μ=0,σ=0.005)的测试图像,(c)是加入椒盐噪声(ρ=O.005)的测试图像。图3~图5分别是对图2中(a)~(c)三幅图像的边缘检测结果。
由实验结果可以看出,SUSAN算法具有以下优良性能:
4.1边缘检测效果好
无论对直线,还是曲线边缘,SUSAN算法基本上可以检测出所有的边缘,检测结果较好。虽然实验中没有达到一个象素的精度,但这主要是因为对边缘的两侧都应用了SUSAN算法,对具体的实际应用,可以对背景不再应用SUSAN算法,这样不但可以达到细化边缘的目的,而且运算量也大大减少。
而Robert算子和Prewitt算子对部分直线边缘不能检测出来,圆的边缘也有部分漏检情况;Gauss-Laplace算子虽然基本上可以检测出所有边缘,但是他的定位效果较差,边缘象素较宽。
4.2抗噪声能力好
由于USAN的求和相当于求积分,所以这种算法对噪声不敏感,而且SUSAN算法不涉及梯度的计算,所以该算法抗噪声的性能很好。很明显,如果考虑有独立同分布的高斯噪声,只要噪声小于USAN函数的相似灰度门限值,噪声就可被忽略。对局部突变的孤立噪声,即使噪声的灰度与核相似,只要局部USAN值小于门限g,也不会对边缘检测造成影响。因此SUSAN边缘检测算法可以用于被噪声污染的图像的边缘检测。
而其他的边缘检测算法,Robert算子、Prewitt算子、Gauss-Laplace算子,以及应用广泛的Canny算子,由于这些算法都涉及一阶梯度,甚至二阶梯度的计算,所以他们的抗噪声能力较差[2-5],图4、图5也证明了这一结论。
边缘是图像最基本的特征,是图像分割的第一步。经典的边缘检测方法如:Roberts,Sobel,Prewitt,Kirsch,Laplace等方法,基本都是对原始图像中象素的小邻域构造边缘检测算子,进行一阶微分或二阶微分运算,求得梯度最大值或二阶导数的过零点,最后选取适当的阀值提取边界。由于这些算法涉及梯度的运算,因此均存在对噪声敏感、计算量大等缺点。在实践中,发现SUSAN算法只基于对周边象素的灰度比较,完全不涉及梯度的运算,因此其抗噪声能力很强,运算量也比较小。并将SUSAN算法用于多类图像的边缘检测中,实验证明该算法非常适合含噪图像的边缘检测。
2 SUSAN边缘检测简介
2.1 SUSAN特征检测原理
如图1所示,用一个圆形模板在图像上移动,若模板内象素的灰度与模板中心象素(称为:核Nucleus)灰度的差值小于一定阀值,则认为该点与核具有相同(或相近)的灰度,由满足这样条件的象素组成的区域称为USAN(Univalue Segment Assimilating Nucleus)。
当圆形模板完全处在图像或背景中时,USAN区域面积最大(如图1中的a和b);当模板移向图像边缘时,USAN区域逐渐变小(如图1中c);当模板中心处于边缘时,USAN区域很小(如图1中的d);当模板中心处于角点时,USAN区域最小(如图1中的e)。可以看出,在边缘处象素的USAN值都小于或等于其最大值的一半。因此,计算图像中每一个象素的USAN值,通过设定一个USAN阀值,查找小于阀值的象素点,即可确定为边缘点[1]。
2.2 SUSAN边缘检测算法
(1)算法描述
对整幅图像中的所有象素,用圆形模板进行扫描,比较模板内每一象素与中心象素的灰度值,通过与给定的阀值比较,来判别该象素是否属于USAN区域,如下式:
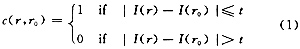
式(1)中c(r,r0)为模板内属于USAN区域的象素的判别函数;I(r0)是模板中心象素(核)的灰度值;I(r)为模板内其他任意象素的灰度值;t是灰度差门限。
图像中每一点的USAN区域大小可用下式表示:
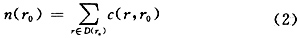
式(2)中D(r0)为以r0为中心的圆形模板区域。得到每个象素的USAN值n(r0)以后,再与预先设定得门限g进行比较,当n(r0)<g时,所检测到象素位置r0可以认为是一个边缘点。
(2)模板的选取
由于图像的数字化,实际上无法实现真正的圆形模板,所以都是采用近似圆代替。但是模板较小时,如果门限选取不恰当,可能会发生边缘点漏检的情况。模板也不宜取得太大,否则会增大运算量大,通常可取5×5或37象素模板[1]。本文实验中均采用的是5×5的模板。
(3)门限t,g的确定
门限g决定了边缘点的USAN区域的最大值,即只要图像中的象素的USAN值小于g,该点就被判定为边缘点。g过大时,边缘点附近的象素可能作为边缘被提取出
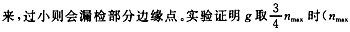 为模板的最大USAN值),可以较好地提取出初始边缘点。如果要达到单象素的精度,还需进一步剔除多余象素。
为模板的最大USAN值),可以较好地提取出初始边缘点。如果要达到单象素的精度,还需进一步剔除多余象素。门限t表示所能检测边缘点的最小对比度,也是能忽略的噪声的最大容限。t越小,可从对比度越低的图像中提取特征。因此对于不同对比度和噪声情况的图像,应取不同的t值[2]。
3 实 验
在主频2.3 GHz,内存256 MB的PC机上,分别对SUSAN算法(t=10,g=18)和传统的Robert算子、Gauss-Laplace算子、Prewitt算子,采用Visal C++编程,对图2中的3幅灰度测试图像进行边缘检测。图2中(a)是原始测试图像,(b)是加入高斯噪声(μ=0,σ=0.005)的测试图像,(c)是加入椒盐噪声(ρ=O.005)的测试图像。图3~图5分别是对图2中(a)~(c)三幅图像的边缘检测结果。
由实验结果可以看出,SUSAN算法具有以下优良性能:
4.1边缘检测效果好
无论对直线,还是曲线边缘,SUSAN算法基本上可以检测出所有的边缘,检测结果较好。虽然实验中没有达到一个象素的精度,但这主要是因为对边缘的两侧都应用了SUSAN算法,对具体的实际应用,可以对背景不再应用SUSAN算法,这样不但可以达到细化边缘的目的,而且运算量也大大减少。
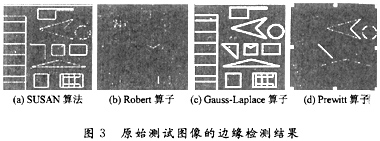


而Robert算子和Prewitt算子对部分直线边缘不能检测出来,圆的边缘也有部分漏检情况;Gauss-Laplace算子虽然基本上可以检测出所有边缘,但是他的定位效果较差,边缘象素较宽。
4.2抗噪声能力好
由于USAN的求和相当于求积分,所以这种算法对噪声不敏感,而且SUSAN算法不涉及梯度的计算,所以该算法抗噪声的性能很好。很明显,如果考虑有独立同分布的高斯噪声,只要噪声小于USAN函数的相似灰度门限值,噪声就可被忽略。对局部突变的孤立噪声,即使噪声的灰度与核相似,只要局部USAN值小于门限g,也不会对边缘检测造成影响。因此SUSAN边缘检测算法可以用于被噪声污染的图像的边缘检测。
而其他的边缘检测算法,Robert算子、Prewitt算子、Gauss-Laplace算子,以及应用广泛的Canny算子,由于这些算法都涉及一阶梯度,甚至二阶梯度的计算,所以他们的抗噪声能力较差[2-5],图4、图5也证明了这一结论。
- 频宽、取样速率及奈奎斯特定理(09-14)
- 为什么要进行信号调理?(09-30)
- IEEE802.16-2004 WiMAX物理层操作和测量(09-16)
- 为任意波形发生器增加价值(10-27)
- 基于PCI 总线的高速数据采集系统(09-30)
- 泰克全新VM6000视频测试仪助力数字电视等产品测试 (10-06)
