时差式超声流量计环鸣法测量的研究

超声流量计

超声流量计是通过检测流体流动对超声束或超声脉冲的作用来测量流量的仪表。作为一种非接触式测量仪表，它相对于传统的流量计而言具有可进行非接触式测量、原理上不受管径限制、其造价基本与管径无关、可测量含有气泡的液体等优点。

对封闭管道用超声流量计来说，按其测量原理可分为传播时间法、多普勒效应法、波束偏移法、相关法等。

本文采用传播时间法。超声波在流体中传播时，与声波在静止流体中传播的速度相比，顺流方向声波传播速度会增大，逆流方向则会减小，同一传播距离就有不同的传播时间。利用传播时间之差与被测流体流速之间的关系求得流速，称为传播时间差法。通过接收穿过流体的超声波就可以检测出流体的流速，从而换算成流量。根据时差的表现形式不同，又可以分为时差法、相位差法和频差法。时差式流量计工作模型如图1所示。



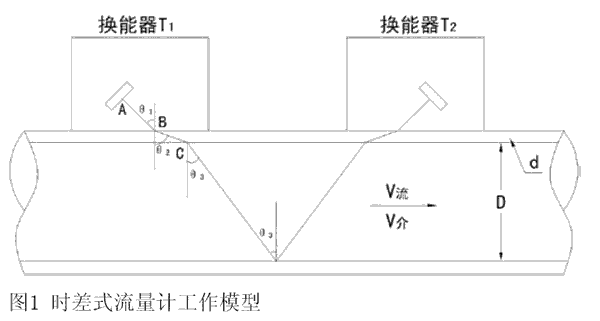
图1中，两个换能器固定在输液管道的同一侧，声波从换能器T1发出，经过输液管道另一侧的内壁，反射到接收换能器T2。两个换能器也可以固定在输液管道的上下两侧，声波由换能器T1发出，直接传播到换能器T2。发射和接收声波的振子密封在换能器的腔体里，其辐射面与端面成一个角度θ1，腔体里用透声材料填充。由于换能器中填充材料、管道材料、管道中流体材料的不同，它们的声速也不同，因此声波传播到介面处会有折射。这里假设折射角为θ2、θ3。流量计在工作时，换能器T1、T2轮流做发射和接收。因为管中的液体是流动的，声波由T1传到T2(正程)和由T2传到T1(逆程)的传播时间是不同的。正程、逆程两个传播时间的差反映出液体的流速、流量。

以换能器T1为例。声波由A到B再传到C，在这一段传播过程中，因为没有流体参与，传播时间是固定不变的。在这里，把声波在换能器填料、管壁中传播时间记为t延。在寻找正程与逆程之间的时间差时，不必考虑t延，只考虑在液体中传播的正程、逆程的传播时间差就可以了。

这里，设D为输液导管内径；d为壁厚；V流为液体流动速度；V介为液体的声速；θ3为折射角；t正为声波由T1到T2的传播时间；t逆为声波由T2到T1的传播时间。

用声学模型可得如下公式：




由上述推导可以看出，只要得到t正和t逆，管道中的液体流速V就可以算出。时差法与频差法和相位差法之间原理方程式的基本关系为：



式中：Δf为频率差；Δφ为相位差；f正、f逆为超声波在流体中顺流和逆流的传播频率；f为超声波的频率。
从中可以看出，相位差法本质上和时差法是相同的，而频率与时间又互为倒数关系，三种方法没有本质的区别。

普通方法测量时间差

所存在问题分析

从上述公式的推导中可以看出，要运用传播时间测流量时，最关键的测量量就是顺逆流传播时间差，只有精确得到这个时间差，流量才能由其导出。

对于小口径、低流速的情况，顺逆流的时差非常短，典型最大流量对应的时差仅约20ns，精确测量难度很大，需要极高的时钟频率。如果测量方法粗放，这个极小的时间量很可能被淹没在测量的误差中。因此，如何才能测量到这个时间量，并使其尽可能精确，就是本文要研究的环鸣法的关键所在。

环鸣法的设计确定

环鸣法的产生

为了解决时间差值太小的的问题，环鸣法利用了让小的量不断积累，使总体值增大，得到总量后再做平均的思想。环鸣法总方框图如图2所示。



该方法中，当换能器T1发射声信号，在换能器T2收到信号的时刻，令T1再次发射声信号，而T2再次接收，这样如此循环发射、接收N次。通过测量记录下N次测量的总时间∑t正。然后，再令T2发射，T1接收，经过N次如此循环就可得到逆向发射总时间∑t逆。这时让顺逆流两个总的时间作差，可以得到总时间差∑Δt。∑Δt这个量比起单次测量时，它已经扩大了2N倍。由测量带来的误差经过了N次累加后，其均值则向零靠近，使得测量精度提高了倍。此时这个值就较容易测量，从而得到想要的流量数据。

环鸣法要解决的几个重要问题

精确捕捉计时点

新测量方法用具有半个周期的正弦脉冲去激励换能器。由于换能器是一个窄带系统，在电脉冲的激励下，发射和接收的声信号都是较短的、有正弦填充的、具有钟形包络的脉冲信号，如图3所示。本文选用冲击信号作发射源，信号持续时间短，因此比较适合细管径的输液管道测量。

正弦函数在过零点处斜率最大。如果把回波的某个正弦周期的过零点检测出来，回波时间的测量精度将极大提高。从总方框图可知，过零点的检测电路是由过零比较器、电平比较器、单稳2电路和与门电路等组成。其波形和信号之间的逻辑关系在图3中可以清楚地看到。



从图3可以看出，得到这个计时点立刻触发单稳1电路以获得发射同步信号。