傅立叶变换、拉普拉斯变换、Z变换最全攻略
时间:01-29
来源:互联网
点击:
傅立叶变换、拉普拉斯变换、Z变换公式
1.傅里叶级数
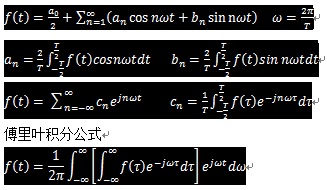
2.非周期傅里叶变换和逆变换

傅里叶变换的性质


3.非周期序列傅里叶变换
1.定义
一个离散时间非周期信号与其频谱之间的关系,可用序列的傅里叶变换来表示。若设离散时间非周期信号为序列x(n),则序列x(n)的傅里叶变换(DTFT)为:
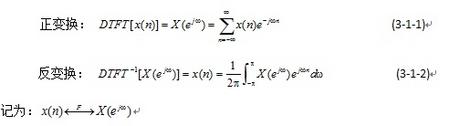
当然式(3-1-2)等式右端的积分区间可以是(0,2π)或其它任何一个周期。
2.离散时间序列傅里叶变换存在的条件:
离散时间序列x(n)的傅里叶变换存在且连续的条件为x(n)满足绝对可和。即:

反之,序列的傅里叶变换存在且连续,则序列一定是绝对可和的。
表3-1给出了常用序列的傅里叶变换,这在以后的实际应用中很重要。
3.1.2 非周期序列傅里叶变换的性质
从序列傅里叶变换定义式(3-1-1)可知,非周期序列的傅里叶变换就是序列的z变换在单位圆上的取值(当序列的z变换在单位圆上收敛时),即:
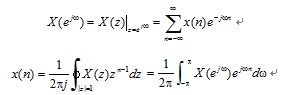
因此,非周期序列傅里叶变换的一切特性,皆可由z变换得到。正因如此,下面所述的性质,读者可仿z变换性质的证明方法进行证明,在这里就不一一证明了。

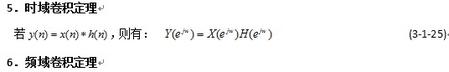

表3-1序列的傅里叶变换的性质
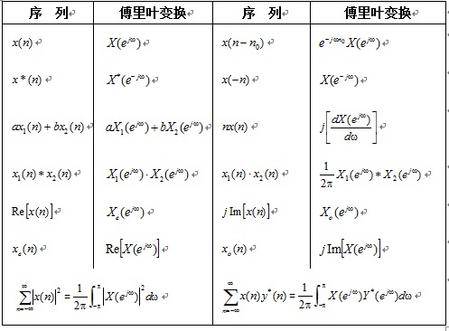
表3-2 常用序列傅里叶变换

4.拉普拉斯变换
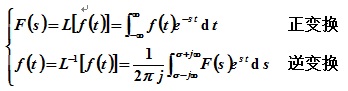
附录A 拉普拉斯变换及反变换
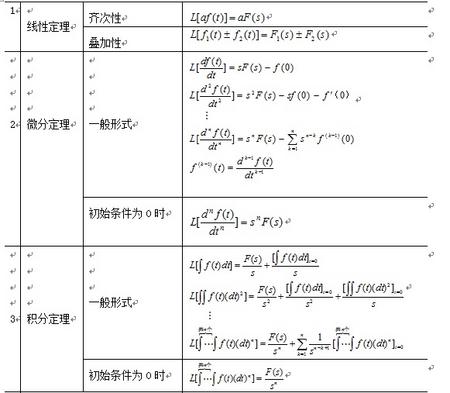
1. 表A-1 拉氏变换的基本性质

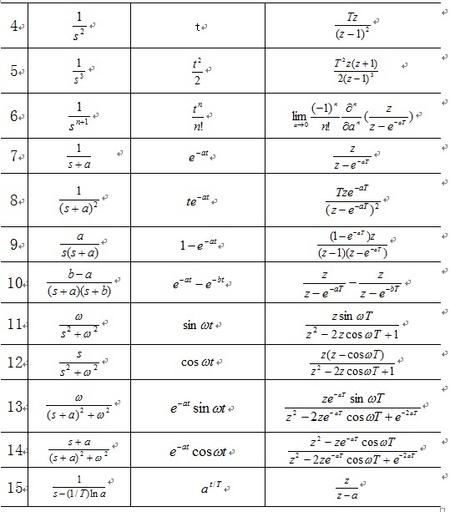
2.表A-2 常用函数的拉氏变换和z变换表

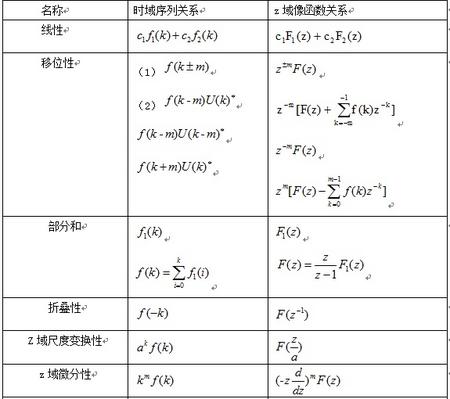
5. Z变换
1 Z变换的定义

常用z变换的基本性质和定理

1.傅里叶级数
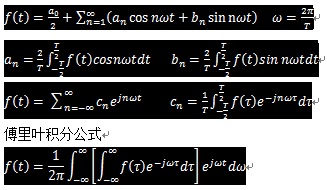
2.非周期傅里叶变换和逆变换

傅里叶变换的性质


3.非周期序列傅里叶变换
1.定义
一个离散时间非周期信号与其频谱之间的关系,可用序列的傅里叶变换来表示。若设离散时间非周期信号为序列x(n),则序列x(n)的傅里叶变换(DTFT)为:
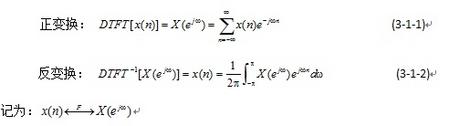
当然式(3-1-2)等式右端的积分区间可以是(0,2π)或其它任何一个周期。
2.离散时间序列傅里叶变换存在的条件:
离散时间序列x(n)的傅里叶变换存在且连续的条件为x(n)满足绝对可和。即:

反之,序列的傅里叶变换存在且连续,则序列一定是绝对可和的。
表3-1给出了常用序列的傅里叶变换,这在以后的实际应用中很重要。
3.1.2 非周期序列傅里叶变换的性质
从序列傅里叶变换定义式(3-1-1)可知,非周期序列的傅里叶变换就是序列的z变换在单位圆上的取值(当序列的z变换在单位圆上收敛时),即:
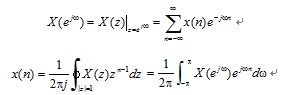
因此,非周期序列傅里叶变换的一切特性,皆可由z变换得到。正因如此,下面所述的性质,读者可仿z变换性质的证明方法进行证明,在这里就不一一证明了。

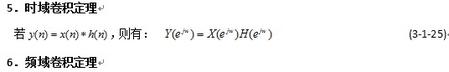

表3-1序列的傅里叶变换的性质

表3-2 常用序列傅里叶变换

4.拉普拉斯变换
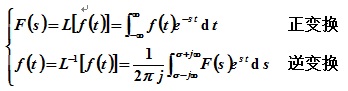
附录A 拉普拉斯变换及反变换
1. 表A-1 拉氏变换的基本性质


2.表A-2 常用函数的拉氏变换和z变换表


5. Z变换
1 Z变换的定义

常用z变换的基本性质和定理


- 如何应对电压开关中常见的挑战(08-26)
- 电源装置的接地系统(11-09)
- 基于LabWindows/CVI的通信电源系统自动化测试的实现(01-23)
- 小型水电站的设备防雷设计(08-28)
- 工控系统的电源抗干扰技术分析(09-25)
- 如何打破UPS电源应用的“坚冰”(02-13)
