直流传感器回馈补偿系统的设计
时间:10-28
来源:互联网
点击:
3 差值电流回馈补偿系统的德定性分析
差值电流回馈补偿系统的开环传递函数为:
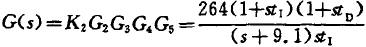
差值补偿电流回馈补偿系统的闭环传递函数为:
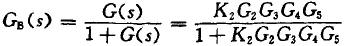
闭环传递函数的特征方程为:
D(s)=sti(s+9.1)+264(1+st1)+(1+stD)
=(264tDt1+t1)s2+(264(tD+t1)+9.1t1)s+264
差值电流回馈补偿系统是一个典型的闭环系统。根据李雅普诺夫稳定性理论,线性系统稳定的充分必要条件是闭环系统特征方程的根都具有负实部,即闭环传递函数的极点均位于坐标平面左半部(不包括虚轴)。但当系统阶次较高时,在一般情况下,求解其特征方程会遇到较大的困难。劳斯及古尔维茨稳定判据,可通过特征方程的根与各项系数的关系来判别系统的特征根是否全部具有负实部,从而分析线性系统的稳定性。
古尔维茨稳定判据求得系统稳定的充要条件:264tDt1+t1>0且264(tD+t1)+9.1t1>0,可见,只要tD>0,t1>0,系统就是稳定的。
4 结 语
磁势自平衡回馈补偿式直流传感器的磁势平衡由铁心的近似矩形磁化曲线决定。其差值电流补偿电路,则是利用双向铁心磁放大器的基本原理,在电抗器铁心的空腔内设置零安匝检测铁心和线圈,用以检测该半周期内直流磁势平衡的安匝差以自动跟踪补偿。根据劳斯阵列的第一列元素符号均为正值可判断差值回馈补偿系统是稳定的。
差值电流回馈补偿系统的开环传递函数为:
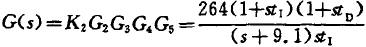
差值补偿电流回馈补偿系统的闭环传递函数为:
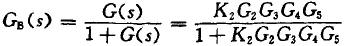
闭环传递函数的特征方程为:
D(s)=sti(s+9.1)+264(1+st1)+(1+stD)
=(264tDt1+t1)s2+(264(tD+t1)+9.1t1)s+264
差值电流回馈补偿系统是一个典型的闭环系统。根据李雅普诺夫稳定性理论,线性系统稳定的充分必要条件是闭环系统特征方程的根都具有负实部,即闭环传递函数的极点均位于坐标平面左半部(不包括虚轴)。但当系统阶次较高时,在一般情况下,求解其特征方程会遇到较大的困难。劳斯及古尔维茨稳定判据,可通过特征方程的根与各项系数的关系来判别系统的特征根是否全部具有负实部,从而分析线性系统的稳定性。
古尔维茨稳定判据求得系统稳定的充要条件:264tDt1+t1>0且264(tD+t1)+9.1t1>0,可见,只要tD>0,t1>0,系统就是稳定的。
4 结 语
磁势自平衡回馈补偿式直流传感器的磁势平衡由铁心的近似矩形磁化曲线决定。其差值电流补偿电路,则是利用双向铁心磁放大器的基本原理,在电抗器铁心的空腔内设置零安匝检测铁心和线圈,用以检测该半周期内直流磁势平衡的安匝差以自动跟踪补偿。根据劳斯阵列的第一列元素符号均为正值可判断差值回馈补偿系统是稳定的。
电流 电路 电子 电感 传感器 二极管 电压 电阻 放大器 相关文章:
- ECL电源开关的应用研究(11-30)
- 电流源电路(01-23)
- 什么是权电流型DAC(数模转换器)(01-24)
- 高速应用中电流反馈运放电路设计分析(01-06)
- 线性光电耦合器在开关电源中的应用(01-15)
- 可对储能器件进行安全且快速充电的通用型电流源(03-13)
