一种基于四阶累积量的自适应均值滤波算法
时间:10-25
来源:互联网
点击:
图像在景物成像、空间采样和量化等过程中经常被外界各种噪声干扰,使图像质量下降。为尽可能减小噪声影响,对降质图像必须进行去噪处理。比较成熟的去噪处理方法有多种,均值滤波是其中非常有效的方法之一。标准均值滤波算法是对图像滤波窗口取平均值代替窗口中心像素点,这样可以在一定程度上抑制噪声。但是这种方法本身存在着以下缺陷:图像细节得不到很好的保护,在去噪的同时也破坏了图像的部分细节,从而使图像变得模糊;对脉冲噪声的消除效果不理想。
1 算法思想
本文提出了一种基于四阶累积量的自适应均值滤波算法,其基本思想是:首先用一个3×3窗口在图像上滑动,计算该窗口内所有像素的四阶累积量,并计算出该窗口中心像素的噪声敏感度系数,根据噪声敏感度系数判断该中心像素是否为噪声点;然后根据3×3窗口中噪声点的个数自适应调整滤波窗口大小;最后采用改进的均值滤波方法对标记为噪声点的像素进行滤波。基于四阶累积量的自适应均值滤波算法在很大程度上保护了图像的细节。同时也抑制了噪声,比标准均值滤波算法具有更好的滤波性能,为消除图像中的噪声提供了一种新的途径。
2 基于四阶累积量的自适应均值滤波算法
基于四阶累积量的自适应均值滤波包括三个过程:根据窗口的四阶累积量计算噪声敏感度系数,并确定图像中噪声点;确定滤波窗口大小;对噪声点进行滤波。
2.1 根据窗口的四阶景积量自适应确定噪声点
确定噪声点是整个滤波算法中最重要的一步,它关系到图像中像素点的正确分类。确定噪声点的方法很多,文献采用3×3窗口确定噪声点,通过计算窗口内所有像素点灰度值的平均值与中心像素点的差值,将该差值与给定的阈值进行比较,差值大于阈值的像素点视为噪声点,否则视为非噪声点。该方法存在以下两个问题:(1)阈值的选择具有很大的随机性,选择太大,噪声消除不干净;选择太小,破坏图像的细节,易使图像模糊。(2)阈值是事先给定的一个固定值,在整个滤波过程中不再变化,该固定的阈值不能真实地反映每个像素点对噪声的敏感程度。文献使用一个K×K的窗口在图像上精动,找出该窗口中灰度的最大值和最小值,如果窗口中心像素灰度值等于最大值或最小值,则确定该像素为噪声点,否则视为非噪声点。该方法的缺点在于:把局部窗口的最大值和最小值作为噪声的判断标准,虽然具有一定的自适应性,但如果该最大值和最小值本身不是噪声点,而以它们为判断噪声的标准,就会把非噪声点误判为噪声点。本文把以上两种方法有机结合起来,采用一种新的方法确定噪声点。
假设图像P大小为M×N,左上角像素点位置为(1,1)。首先找出整幅图像灰度值的最大值和最小值,分别记为Max(PM×N)和Min(PM×N)。在确定噪声点时仍采用3×3窗口在图像上滑动,该窗口中心像素点灰度值为g(i,j),则该窗口内所有像素值构成如下集合:

噪声点标记为F(i,j)=1,非噪声点标记为F(i,j)=O。对于上述方法,方法(1)和(2)很容易实现,方法(3)实现的难点在于如何确定阚值Ti,j,因为Ti,j对于图像滤波质量有非常重要影响。本文提出基于四阶累积量的噪声敏感度系数来确定阈值Ti,j。
在本文中定义的噪声敏感度系数是人类视觉系统刚好能够感受到的图像噪声的临界值,用β表示。在文献中选用了标准差来定义β;在文献中通过计算像素点r阶中心矩来定义β。本文中,通过计算四阶累积量对β进行定义,这是因为文献和文献所定义的β比较粗糙,而四阶累积量可以得到比标准差更多的信息。βi,j是β矩阵的(i,j)元素值,表示窗口Si,j中心像素
点(i,j)的噪声敏感度系数。
假设一个均值为零的实值信号s(t),它的概率密度函数为p(s),K[p(s)]是信号规范的四阶累积量,其定义式如下:

其中n2表示窗口的大小,本文中
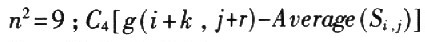
表示窗口像素对于该窗口均值差值的四阶累积量,这是为了使窗口子图像变为均值为零的信号。把噪声敏感度系数做为判断噪声点的阈值,即Ti,j=βi,j。每个像素是否为噪声点,只要计算中心像素的噪声敏感度系数,然后判断是否
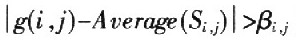
即可。
2.2 自适应确定滤波窗口大小
标准均值滤波算法的平均效果会引起图像模糊。模糊程度和滤波窗口大小成正比,选择较小的滤波窗口能保护图像细节部分,但是去噪能力较弱;选择较大的滤波窗口虽然能得到较强的去噪能力,但是图像会变得模糊。根据这些特点,本文结合小窗口滤波和大窗口滤波两方面的优势,根据窗口内噪声点的个数,自适应确定滤波窗口大小。
在统计噪声点个数时,仍然采用3×3窗口。在确定窗口中心像素为噪声点的情况下,统计公式如下:

其中FWi,j表示像素点(i,j)滤波窗口的大小,它只与3×3窗口内噪声点个数有关。
1 算法思想
本文提出了一种基于四阶累积量的自适应均值滤波算法,其基本思想是:首先用一个3×3窗口在图像上滑动,计算该窗口内所有像素的四阶累积量,并计算出该窗口中心像素的噪声敏感度系数,根据噪声敏感度系数判断该中心像素是否为噪声点;然后根据3×3窗口中噪声点的个数自适应调整滤波窗口大小;最后采用改进的均值滤波方法对标记为噪声点的像素进行滤波。基于四阶累积量的自适应均值滤波算法在很大程度上保护了图像的细节。同时也抑制了噪声,比标准均值滤波算法具有更好的滤波性能,为消除图像中的噪声提供了一种新的途径。
2 基于四阶累积量的自适应均值滤波算法
基于四阶累积量的自适应均值滤波包括三个过程:根据窗口的四阶累积量计算噪声敏感度系数,并确定图像中噪声点;确定滤波窗口大小;对噪声点进行滤波。
2.1 根据窗口的四阶景积量自适应确定噪声点
确定噪声点是整个滤波算法中最重要的一步,它关系到图像中像素点的正确分类。确定噪声点的方法很多,文献采用3×3窗口确定噪声点,通过计算窗口内所有像素点灰度值的平均值与中心像素点的差值,将该差值与给定的阈值进行比较,差值大于阈值的像素点视为噪声点,否则视为非噪声点。该方法存在以下两个问题:(1)阈值的选择具有很大的随机性,选择太大,噪声消除不干净;选择太小,破坏图像的细节,易使图像模糊。(2)阈值是事先给定的一个固定值,在整个滤波过程中不再变化,该固定的阈值不能真实地反映每个像素点对噪声的敏感程度。文献使用一个K×K的窗口在图像上精动,找出该窗口中灰度的最大值和最小值,如果窗口中心像素灰度值等于最大值或最小值,则确定该像素为噪声点,否则视为非噪声点。该方法的缺点在于:把局部窗口的最大值和最小值作为噪声的判断标准,虽然具有一定的自适应性,但如果该最大值和最小值本身不是噪声点,而以它们为判断噪声的标准,就会把非噪声点误判为噪声点。本文把以上两种方法有机结合起来,采用一种新的方法确定噪声点。
假设图像P大小为M×N,左上角像素点位置为(1,1)。首先找出整幅图像灰度值的最大值和最小值,分别记为Max(PM×N)和Min(PM×N)。在确定噪声点时仍采用3×3窗口在图像上滑动,该窗口中心像素点灰度值为g(i,j),则该窗口内所有像素值构成如下集合:

噪声点标记为F(i,j)=1,非噪声点标记为F(i,j)=O。对于上述方法,方法(1)和(2)很容易实现,方法(3)实现的难点在于如何确定阚值Ti,j,因为Ti,j对于图像滤波质量有非常重要影响。本文提出基于四阶累积量的噪声敏感度系数来确定阈值Ti,j。
在本文中定义的噪声敏感度系数是人类视觉系统刚好能够感受到的图像噪声的临界值,用β表示。在文献中选用了标准差来定义β;在文献中通过计算像素点r阶中心矩来定义β。本文中,通过计算四阶累积量对β进行定义,这是因为文献和文献所定义的β比较粗糙,而四阶累积量可以得到比标准差更多的信息。βi,j是β矩阵的(i,j)元素值,表示窗口Si,j中心像素
点(i,j)的噪声敏感度系数。
假设一个均值为零的实值信号s(t),它的概率密度函数为p(s),K[p(s)]是信号规范的四阶累积量,其定义式如下:

其中n2表示窗口的大小,本文中
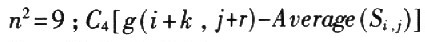
表示窗口像素对于该窗口均值差值的四阶累积量,这是为了使窗口子图像变为均值为零的信号。把噪声敏感度系数做为判断噪声点的阈值,即Ti,j=βi,j。每个像素是否为噪声点,只要计算中心像素的噪声敏感度系数,然后判断是否
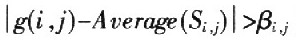
即可。
2.2 自适应确定滤波窗口大小
标准均值滤波算法的平均效果会引起图像模糊。模糊程度和滤波窗口大小成正比,选择较小的滤波窗口能保护图像细节部分,但是去噪能力较弱;选择较大的滤波窗口虽然能得到较强的去噪能力,但是图像会变得模糊。根据这些特点,本文结合小窗口滤波和大窗口滤波两方面的优势,根据窗口内噪声点的个数,自适应确定滤波窗口大小。
在统计噪声点个数时,仍然采用3×3窗口。在确定窗口中心像素为噪声点的情况下,统计公式如下:

其中FWi,j表示像素点(i,j)滤波窗口的大小,它只与3×3窗口内噪声点个数有关。
- 12位串行A/D转换器MAX187的应用(10-06)
- AGC中频放大器设计(下)(10-07)
- 低功耗、3V工作电压、精度0.05% 的A/D变换器(10-09)
- PIC16C5X单片机睡眠状态的键唤醒方法(11-16)
- 用简化方法对高可用性系统中的电源进行数字化管理(10-02)
- 利用GM6801实现智能快速充电器设计(11-20)
