运算放大器电路固有噪声的分析与测量：噪声测量实例2

测量 OPA227 的低频噪声

许多产品说明书都规定了从 0.1 Hz 到 10 Hz 的峰至峰噪声参数。这有效地给出了运算放大器的低频（也就是 1/f 噪声）概念。在一些情况下将以示波器波形形式给出；而在其它情况下，则以参数表形式列出。图 6.10 显示了一种测量从 0.1Hz 到 10Hz 噪声的有效方法。该电路采用了二阶 0.1Hz 高通与四阶 10Hz 低通串联滤波器，增益为 100。所测设备 (OPA227) 置于高增益配置（噪声增益=1001）下，因为预计 1/f 噪声很小，并且必须放大到可用标准测试设备进行测量的范围内。请注意，图 6.10 中电路的总增益为 100100（也就是 100x1001）。因此，输出信号应除以 100100 以将信号复原到输入。



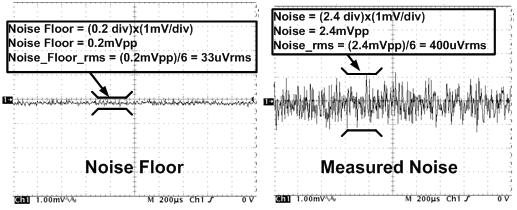
图 6.10：示波器显示的结果

图 6.11 中所示电路的所测输出如图 6.12 所示。图 6.12 为从 OPA227 产品说明书中截取的一张图表。所测结果的范围可除以总增益，以得出运算放大器的输入范围（也就是，5mV/100100 = 50nV）。请注意，实际产品说明书曲线与期望的产品说明书曲线有很好的一致性。



图 6.11：低频噪声测量测试电路



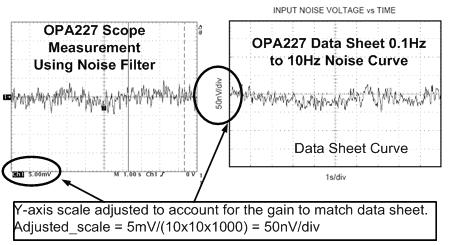
图 6.12：低频噪声测量测试电路结果

低频噪声测量中的失调温度漂移与 1/f 噪声的关系

测量放大器 1/f 噪声的一个难题是：我们通常很难将 1/f 噪声与失调温度漂移分离开来。请注意，在典型的实验室环境下，周围环境温度会有 ±3C 的波动。设备周围的气流会造成失调电压的低频变化，与 1/f 噪声看上去很类似。图 6.12 比较了 OPA132 在热稳定环境下与在典型实验室环境下的输出。假设最坏情况下的运算放大器漂移，在典型实验室环境下，失调电压漂移将为 60uV 左右（根据产品说明书(10uV/C)(6C) = 60uV）。图 6.12 中的放大器增益为 100，因此输出漂移的近似值为 6mV（即 (60uV)(100) = 6mV）。

将失调电压漂移的效应从 1/f 噪声中分离开来的一种方法是将所测设备置入一个热稳定环境中。该环境必须在整个测量过程中，都保持设备的温度恒定（变化范围在 ±0.1C 内），并且也应尽可能减少温度梯度。实现该目的的一个简单方法是将电子惰性填充液注入到漆罐中，并在整个测试过程中都将设备浸在液体中。热传导氟化液通常可用于该类型的测试，因为它们的电阻很高，热阻抗也很高。并且，它们也是生物惰性材料，并且无毒性。



图 6.13： OPA132 在实验室与热稳定环境中的表现

测量 OPA627 的噪声频谱密度曲线

正如我们在本丛书中见到的，在噪声分析中频谱密度参数是一种特别重要的工具。尽管绝大多数的产品说明书都提供了该信息，但工程师有时也会进行实际测量，以验证公布的数据。图 6.14 中的电路显示了一种简单的测试结构，可以对电压噪声频谱密度进行测量。

请注意，用于本测量的频谱分析仪的带宽是从 0.064Hz 到 100kHz。这样的带宽范围可对许多放大器的 1/f 区和宽带区进行特征测量。此外，请注意频谱分析仪内部配置为直流耦合模式，而不是交流耦合模式，因为它的下限截止频率为 1Hz，1/f时的读数精度不高。然而，还是应将运算放大器电路与频谱分析仪进行交流耦合，因为相对噪声来说，直流失调电压很大。因此，运算放大器电路结合使用外部耦合电容 C1 和频谱分析仪的输入阻抗 R3 进行交流耦合。该电路的下限截止频率为 0.008Hz（这对我们的 1/f 测量不会造成干扰，因为频谱分析仪的最小频率为 0.064Hz）。请注意 C1 实际上是并联的多个陶瓷电容（不推荐在本应用中使用电解质电容和钽电容）。

图 6.14 中放大器配置的另一个考虑因素是反馈网络的值。第 3 部分中我们说过并联 R1 和 R2 (Req = R1||R2) 用于热噪声和偏置电流噪声的计算。该阻抗的数值应最小化，以使得所测噪声为运算放大器电压噪声（也就是说，偏置电流噪声和电阻热噪声的影响可忽略不计）。



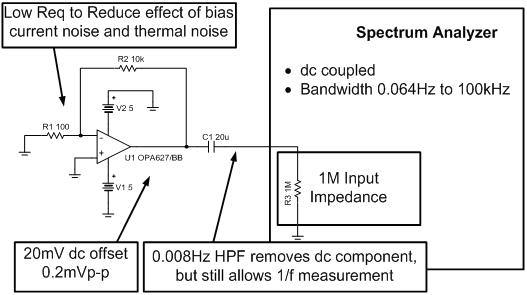
图 6.14：运算放大器噪声频谱密度的测量电路

在所有的噪声测量中，要检验频谱分析仪的噪声底限是否小于运算放大器电路。图 6.14 所示例子中，放大器的增益是 100，以将输出噪声提高到频谱分析仪的噪声底限之上。请谨记该配置会限制高频带宽（带宽=增益带宽乘积/增益=16MHz/100=160kHz），从而，噪声频谱密度曲线将在较低频率时呈现下降趋势。图 6.14 中的例子并不受这一问题的影响，因为高频下降趋势在频谱分析仪带宽之外产生（噪声频谱下降趋势出现在 160kHz，而频谱分析仪的最大带宽是 100kHz）。

图 6.15 显示了频谱分析仪的测量结果。请注意，数据是在数个不同的频率范围采集的（0.064 Hz 到 10 Hz，10 Hz 到 1 kHz，以及 1 kHz 到 100 kHz）。这是因为本例中的频谱分析仪使用了线性频率扫描对数据进行采集。例如，如果每隔 0.1Hz 采集一个数据点，则在低频时精度将太差，而在高频时精度又将超出要求。并且在宽泛的频率范围内使用低精度也要求特别多的数据点（比如，0.1Hz 的精度与 100kHz 的带宽要求 1x106 点）。另一方面，如果您对不同的频率使用不同的精度，则您可以在每个频率范围内均获得很好的精度，而不需要使用特别多的数据点。例如，从 0.064 Hz 到 10 Hz 的精度可设置为 0.01Hz，而从 1kHz 到 100kHz 的精度则可设置为 100Hz。



图 6.15：测量不同频率范围上的频谱密度

图 6.16 突出了在频谱分析仪测量结果中的常见异常。第一个异常是来自外部的噪声拾取。本例特别显示了 60Hz 以及 120Hz 时的噪声拾取。频谱分析仪的内部振荡器也会产生噪声。在理想的环境下，通过屏蔽，可以将噪声拾取降到最小。不过，实际中噪声拾取通常是不可避免的。关键问题在于要确定频谱中的噪声“脉冲”是不是由噪声拾取引起的，或者是确定其是不是设备固有噪声频谱密度的组成部分。

图 6.15 中所示的频谱密度曲线中的另一个常见异常是在给定测量频率范围内，最小频率处产生的相对较大的误差。为了更好地理解该误差，我们可以认为频谱测量是通过在整个频谱内扫描带通滤波器完成的。例如，假设频率范围是从 1Hz 到 1kHz，并且带通滤波器的分辨率带宽是 1Hz。在该频率范围内，带通滤波器的分辨率带宽在高频处相对较窄，而在低频处相对较宽。现在可以考虑带通滤波器的边缘在低频时从 1/f 噪声引入较大误差。图 6.17 图示了该误差。

理解不同的测量异常可以对误差进行矫正。比如，通过在几个频率范围上测量数据，并在频率范围低端去掉几个数据点，您可以得出更精确的结果。在我们的例子中，从 0.0625 Hz 到 10 Hz 的频率范围与 10 Hz 到 1 kHz 的频率范围交迭。（10Hz, 1kHz）频率范围包含了一些 10Hz 以下的错误数据，因此要去掉这些错误数据。在频谱密度测量中可以省略掉噪声拾取（比如，60Hz 的噪声），因为它不是运算放大器固有噪声的组成部分。

图 6.18 显示了本例所测量的噪声频谱密度曲线，去掉了异常读数。图 6.18 中的数据还要除以所测电路增益，以使频谱密度指示运算放大器输入。最后，对数据进行了平均。



图 6.16：频谱密度测量结果的常见异常



图 6.17：最小频率处的测量结果，包括误差在内



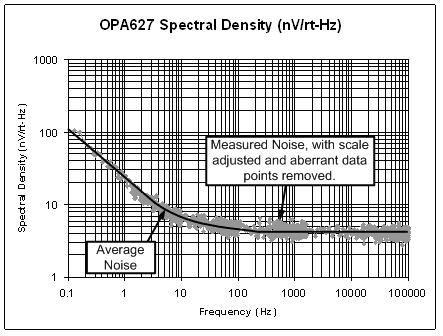
图 6.18：频谱密度测量结果

将 OPA627 的频谱密度测量与产品说明书中的曲线进行比较，我们发现了一个有趣的结果。宽带噪声的测量结果和产品说明书中的参数非常吻合，但是 1/f 噪声测量则与参数有很大不同。事实上，1/f 噪声与参数的偏差并不令我们感到很意外。在本丛书的第 7 部分，我们将详细讨论这一问题。



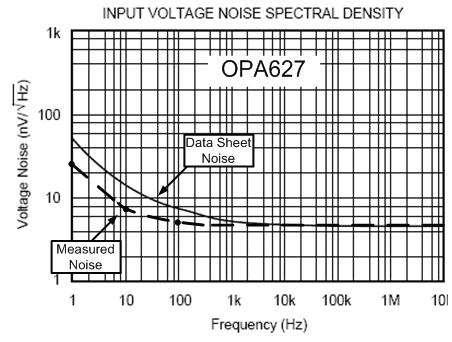
图 6.19：所测的频谱密度与产品说明书中参数的比较