基于TMS320C64x实现LFM信号的实时脉冲压缩
时间:09-16
来源:互联网
点击:
1 引言
脉冲压缩技术因解决了雷达作用距离与分辨率之间的矛盾而成为现代雷达的一种重要体制,数字LFM(线性调频)信号脉冲压缩就是利用数字信号处理的方法来实现雷达信号的脉冲压缩,脉冲压缩器的设计就是匹配滤波器的设计,脉冲压缩过程是接收信号与发射波形的复共扼之间的相关函数,在时域实现时,等效于求接收信号与发射信号复共轭的卷积。若考虑到抑制旁瓣加窗函数,不但要增加存储器,而且运算量将增加1倍,在频域实现时,是接收信号的FFT值与发射波形的FFT值的复共轭相乘,然后再变换到时域而获得的。若求N点数字信号的脉冲压缩,频域算法运算量大大减少,而且抑制旁瓣加窗时不需增加存储器及运算量,相比较而言,用频域FFT实现脉冲压缩的方法较优,因此选用频域方法来实现脉冲压缩,但是仍需要做大量的运算。
2 脉冲压缩系统工业原理
2.1 用FFT法实现LFM信号的数字脉冲压缩
时域脉冲压缩的过程是通过对接收信号s(t)与匹配滤波器脉冲响应求卷积的方法实现的,根据匹配滤波理论,h(t)=s*(t0-t),即匹配滤波器是输入信号的共轭镜像,并有相应的时移t0。则压缩网络的冲激响应为:
h(n)=s*(N-n ) (1)
式中:n=0,1,…,N-1;N表明当发射波形是有限宽度时,冲激响应也是一个有限序列。 根据卷积定理,并采用N点DFT,则可得压缩网络的输出;
y(n)=ID{D[s(n)D[s*(N-n)]} (2)
如采用FFT算法,则可得用FFT法实现数字式脉冲压缩的数字模型为:
y(n)=IFFT{FFT[s(n)FFT[s*(N-n)]} (3)
当N=0时,y(n)=IFFT(|FFTs(n)|2)
LFM信号的突出优点是匹配滤波器对回波信号的多普勒频移不敏感,即使回波信号有较大的多普勒频移,原来的匹配滤波器仍能起到脉冲压缩的使用,这将大大简化信号处理系统,LFM信号经匹配滤波器后的输出脉冲y(t)具有sinc(t)函数型包络,其最大副瓣电平为主瓣电压的13.2dB。
频域快速卷积法数字脉压压缩原理如图1所示。
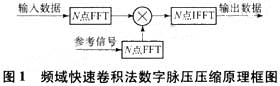
2.2 数字式LFM信号的形成
LFM信号是一种瞬时频率随时间呈线性变化的信号,LFM矩形脉冲信号的复数表达式为:

I(n)、Q(n)分别看作是匹配滤波器系数的实部和虚部,预先计算出来,存储在存储器中,计算时方便调用。
产生LFM信号的方法如图2所示。
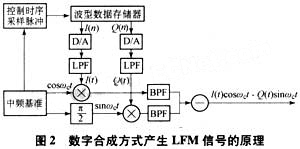
3 LFM信号实时脉冲压缩的实现
3.1 TMS320C64x处理器特点
TMS320C64x是TI公司最新推出的高性能DSP,其时钟频率可达600MHz,最高处理能力为4800MIPS(百万次指令每秒),软件与C62X完全兼容,每个时钟周期可以执行8条指令。TMS320C64x采用TI公司独有的VelociTI结构,这是一种改进哈佛结构、超长指令字的CPU。这种结构使得TMS320C64x超过了传统超标量设计CPU的性能。
TMS320C64x处理器的特点:
a)具有8个功能单元的先进的超常指令字,包括2个乘法器和6个算术单元,在统一个指令周期内可最高同时执行8条指令,是通常CPU的10倍。允许用户开发出有效的类似于精简指令集计算机(RISC)的代码,以得到更高的性能。
b)指令打包,使得并行执行的8条代码长度保持一致性,同时减小了代码长度、取指令时间和功率消耗。
c)所有的指令都具有条件可执行的性能,从而减少了分支开销,提高了并行运算的性能,峰值1600MIPS的指令执行速度,峰值1 GFLOPS(10亿次浮点运算每秒)。
d)业界最有效的C代码编译器、优化器使得软件开发有不可比拟的优越性。
e)片内64KB数据存储器,64KB可配置为高速缓存模式的程序存储器。统一编址的片外2GB地址空间提供对所有存储器类型、数据宽度的有效支持,具有无粘着的存储器接口及各种DRAM刷新逻辑。
3.2 程序流程
脉冲压缩实现的流程图如图3所示。
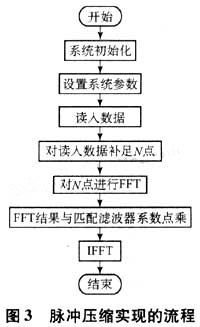
在运算过程中所有数据采用32点浮点型数据,最后脉冲压缩的精度铺可达10-5。其中IFFT可以完全不改变FFT程序而直接调用,IDFT如下:
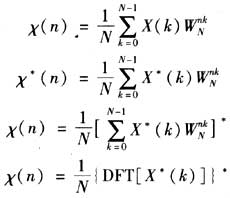
先将X(k)取共轭,直接利用FFT程序,最后将运算结果取一次共轭,以乘以1/N。
3.3 算法优化
TMS320C64x提供了可以同时操作的8个运算单元,可以同时完成4个输入数据的2个和、差或者完成2个32bit乘法,这对于在本系统中FFT/IFFT运算的大量蝶型运算具有很大的意义,配合硬件流水线,TMS320C64x可以不间断的流水完成批量数据的FFT/IFFT,最好情况下单周期可以完全8次定点操作,大大降低了整个程序的时钟周期数。
IFFT运算中第1次求共轭通过一次的算术变型在点乘的那一步就可以实现,以减少指令周期数,原理如下,设I1,Q1为接收回波数据FFT后的结果;I2,Q2为匹配滤波器求共轭后的结果,存储在DRAM中,则有
A=(I1+JQ1)·(I2+jQ2)=I1·I2-Q1·Q2+j[I1·Q2+Q1·I2]
A*=I1·I2-Q1·Q2+j[-I1·Q2-Q1·I2]=I1·I2+Q1·(-Q2)+j[I1·(-Q2)-Q1·I2]
可得若将存储在DRAM中的匹配滤波器求共轭后的结果(I1+jQ2)改存为(I2-jQ2)即不取共轭;在实现点乘的指令中把实部、虚部中符号变号即可。
脉冲压缩技术因解决了雷达作用距离与分辨率之间的矛盾而成为现代雷达的一种重要体制,数字LFM(线性调频)信号脉冲压缩就是利用数字信号处理的方法来实现雷达信号的脉冲压缩,脉冲压缩器的设计就是匹配滤波器的设计,脉冲压缩过程是接收信号与发射波形的复共扼之间的相关函数,在时域实现时,等效于求接收信号与发射信号复共轭的卷积。若考虑到抑制旁瓣加窗函数,不但要增加存储器,而且运算量将增加1倍,在频域实现时,是接收信号的FFT值与发射波形的FFT值的复共轭相乘,然后再变换到时域而获得的。若求N点数字信号的脉冲压缩,频域算法运算量大大减少,而且抑制旁瓣加窗时不需增加存储器及运算量,相比较而言,用频域FFT实现脉冲压缩的方法较优,因此选用频域方法来实现脉冲压缩,但是仍需要做大量的运算。
2 脉冲压缩系统工业原理
2.1 用FFT法实现LFM信号的数字脉冲压缩
时域脉冲压缩的过程是通过对接收信号s(t)与匹配滤波器脉冲响应求卷积的方法实现的,根据匹配滤波理论,h(t)=s*(t0-t),即匹配滤波器是输入信号的共轭镜像,并有相应的时移t0。则压缩网络的冲激响应为:
h(n)=s*(N-n ) (1)
式中:n=0,1,…,N-1;N表明当发射波形是有限宽度时,冲激响应也是一个有限序列。 根据卷积定理,并采用N点DFT,则可得压缩网络的输出;
y(n)=ID{D[s(n)D[s*(N-n)]} (2)
如采用FFT算法,则可得用FFT法实现数字式脉冲压缩的数字模型为:
y(n)=IFFT{FFT[s(n)FFT[s*(N-n)]} (3)
当N=0时,y(n)=IFFT(|FFTs(n)|2)
LFM信号的突出优点是匹配滤波器对回波信号的多普勒频移不敏感,即使回波信号有较大的多普勒频移,原来的匹配滤波器仍能起到脉冲压缩的使用,这将大大简化信号处理系统,LFM信号经匹配滤波器后的输出脉冲y(t)具有sinc(t)函数型包络,其最大副瓣电平为主瓣电压的13.2dB。
频域快速卷积法数字脉压压缩原理如图1所示。

2.2 数字式LFM信号的形成
LFM信号是一种瞬时频率随时间呈线性变化的信号,LFM矩形脉冲信号的复数表达式为:

I(n)、Q(n)分别看作是匹配滤波器系数的实部和虚部,预先计算出来,存储在存储器中,计算时方便调用。
产生LFM信号的方法如图2所示。

3 LFM信号实时脉冲压缩的实现
3.1 TMS320C64x处理器特点
TMS320C64x是TI公司最新推出的高性能DSP,其时钟频率可达600MHz,最高处理能力为4800MIPS(百万次指令每秒),软件与C62X完全兼容,每个时钟周期可以执行8条指令。TMS320C64x采用TI公司独有的VelociTI结构,这是一种改进哈佛结构、超长指令字的CPU。这种结构使得TMS320C64x超过了传统超标量设计CPU的性能。
TMS320C64x处理器的特点:
a)具有8个功能单元的先进的超常指令字,包括2个乘法器和6个算术单元,在统一个指令周期内可最高同时执行8条指令,是通常CPU的10倍。允许用户开发出有效的类似于精简指令集计算机(RISC)的代码,以得到更高的性能。
b)指令打包,使得并行执行的8条代码长度保持一致性,同时减小了代码长度、取指令时间和功率消耗。
c)所有的指令都具有条件可执行的性能,从而减少了分支开销,提高了并行运算的性能,峰值1600MIPS的指令执行速度,峰值1 GFLOPS(10亿次浮点运算每秒)。
d)业界最有效的C代码编译器、优化器使得软件开发有不可比拟的优越性。
e)片内64KB数据存储器,64KB可配置为高速缓存模式的程序存储器。统一编址的片外2GB地址空间提供对所有存储器类型、数据宽度的有效支持,具有无粘着的存储器接口及各种DRAM刷新逻辑。
3.2 程序流程
脉冲压缩实现的流程图如图3所示。

在运算过程中所有数据采用32点浮点型数据,最后脉冲压缩的精度铺可达10-5。其中IFFT可以完全不改变FFT程序而直接调用,IDFT如下:
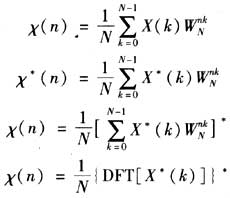
先将X(k)取共轭,直接利用FFT程序,最后将运算结果取一次共轭,以乘以1/N。
3.3 算法优化
TMS320C64x提供了可以同时操作的8个运算单元,可以同时完成4个输入数据的2个和、差或者完成2个32bit乘法,这对于在本系统中FFT/IFFT运算的大量蝶型运算具有很大的意义,配合硬件流水线,TMS320C64x可以不间断的流水完成批量数据的FFT/IFFT,最好情况下单周期可以完全8次定点操作,大大降低了整个程序的时钟周期数。
IFFT运算中第1次求共轭通过一次的算术变型在点乘的那一步就可以实现,以减少指令周期数,原理如下,设I1,Q1为接收回波数据FFT后的结果;I2,Q2为匹配滤波器求共轭后的结果,存储在DRAM中,则有
A=(I1+JQ1)·(I2+jQ2)=I1·I2-Q1·Q2+j[I1·Q2+Q1·I2]
A*=I1·I2-Q1·Q2+j[-I1·Q2-Q1·I2]=I1·I2+Q1·(-Q2)+j[I1·(-Q2)-Q1·I2]
可得若将存储在DRAM中的匹配滤波器求共轭后的结果(I1+jQ2)改存为(I2-jQ2)即不取共轭;在实现点乘的指令中把实部、虚部中符号变号即可。
- 无需调谐的“砖墙式”低通音频滤波器(11-20)
- 视频有源滤波器 (11-26)
- 通用和低噪声的有源滤波器提供达10MHz的可重复性能(01-05)
- 直流耦合视频放大器/滤波器的视频信号电平转换(07-03)
- 开关电容梳状滤波器幅频特性的深入分析(06-05)
- 在高温超导滤波器后级的低温低噪声放大器的设计和调试方法(06-01)
