运算放大器电路中固有噪声的分析与测量
时间:09-14
来源:互联网
点击:
我们可将噪声定义为电子系统中任何不需要的信号。噪声会导致音频信号质量下降以及精确测量方面的错误。板级与系统级电子设计工程师希望能确定其设计方案在最差条件下的噪声到底有多大,并找到降低噪声的方法以及准确确认其设计方案可行性的测量技术。
噪声包括固有噪声及外部噪声,这两种基本类型的噪声均会影响电子电路的性能。外部噪声来自外部噪声源,典型例子包括数字开关、60Hz 噪声以及电源开关等。固有噪声由电路元件本身生成,最常见的例子包括宽带噪声、热噪声以及闪烁噪声等。本系列文章将介绍如何通过计算来预测电路的固有噪声大小,如何采用 SPICE模拟技术,以及噪声测量技术等。
热噪声
热噪声由导体中电子的不规则运动而产生。由于运动会随温度的升高而加剧,因此热噪声的幅度会随温度的上升而提高。我们可将热噪声视为组件(如电阻器)电压的不规则变化。图 1.1 显示了标准示波器测得的一定时域中热噪声波形,我们从图中还可看到,如果从统计学的角度来分析随机信号的话,那么它可表现为高斯分布曲线。我们给出分布曲线的侧面图,从中可以看出它与时域信号之间的关系。
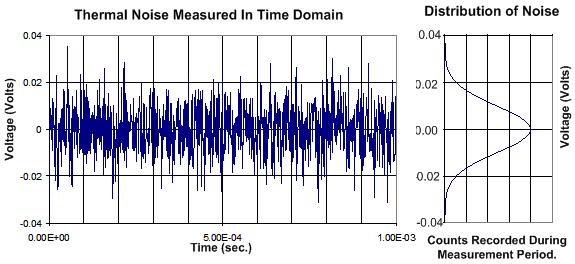
图 1.1: 在时间域中显示白噪声以及统计学分析结果
热噪声信号所包含的功率与温度及带宽直接成正比。请注意,我们可简单应用功率方程式来表达电压与电阻之间的关系 (见方程式1.1),根据该表达式,我们可以估算出电路均方根 (RMS) 噪声的大小。此外,它还说明了在低噪声电路中尽可能采用低电阻元件的重要性。

方程式 1.1:热电压
方程式 1.1 中有一点值得重视的是,根据该表达式我们还可计算出 RMS 噪声电压。在大多数情况下,工程师希望了解“最差条件下噪声会有多严重?”换言之,他们非常关心峰峰值电压的情况。如果我们要将 RMS 热噪声电压转化为峰峰值噪声的话,那么必须记住的一点是:噪声会表现为高斯分布曲线。这里有一些单凭经验的方法即根据统计学上的关系,我们可将 RMS 热噪声电压转化为峰峰值噪声。不过,在介绍有关方法前,我想先谈谈一些数学方面的基本原理。本文的重点在于介绍统计学方面的基本理论,随后几篇文章将讨论实际模拟电路的测量与分析事宜。
概率密度函数:
构成正态分布函数的数学方程式称作“概率密度函数”(见方程式 1.2)。根据一段时间内测得的噪声电压绘制出相应的柱状图,从该柱状图,我们可以大致看出函数所表达的形状。图 1.2 显示了测得的噪声柱状图,并给出了相应的概率密度函数。

方程式 1.2: 高斯曲线分布曲线对应的概率密度函数
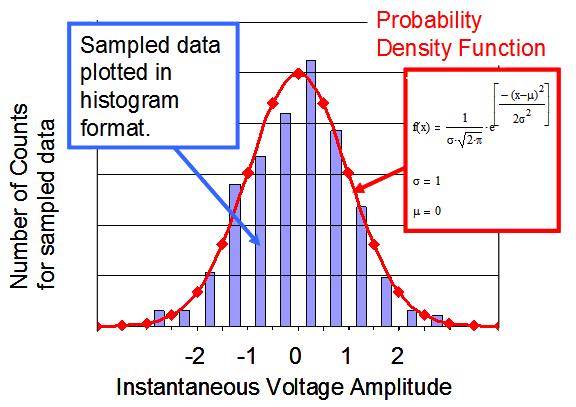
图1.2: 根据相应的概率密度函数所绘制的分布曲线
概率分布函数:
概率分布函数是概率密度函数的积分。根据该函数,我们可了解某事件在给定的时间段内发生的概率(见方程式 1.3 与图 1.3)。举例来说,我们可以假定图 1.4 为噪声概率分布函数,该函数告诉我们,在任意时间点上,在 -1V 与 +1V 之间(即 (-1, 1) 区间内)检测到噪声电压的概率为 30%。

方程式 1.3: 概率分布函数

图 1.3: 概率密度函数与概率分布函数
概率分布函数对我们将RMS热噪声电压转化为峰峰值噪声非常有用。请注意,高斯分布曲线的尾部是无限延伸的,这就是说,任何噪声电压都是可能的。尽管理论上确实如此,但就实际情况而言,极大的瞬时噪声电压发生的可能性不大。举例来说,我们检测到噪声电压在 -3σ 与 +3σ 之间的概率为 99.7 %。换言之,噪声电压超出该范围的概率仅有0.3 %。因此,我们通常将噪声信号的峰值估算为±3σ(即 6σ)。请注意,也有些工程师将噪声的峰值估算为 6.6σ。人们对到底如何估计这个数值没有定论。图 1.4 显示,68% 的噪声都会不超过 2σ。表 1.1 总结了测量噪声电压时标准偏差与概率之间的关系。
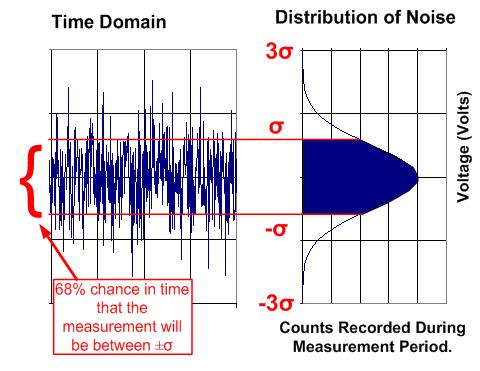
图 1.4: 标准偏差与峰值噪声间的关系
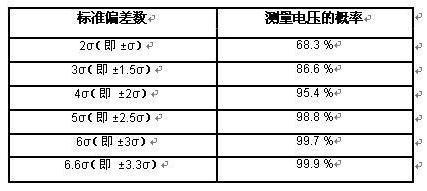
表 1.1: 标准偏差数与测量概率百分比
因此,在一定的标准偏差条件下,我们可以根据关系式来估算峰值对峰值噪声。不过,总体来说,我们还是希望将 RMS 噪声电压转化为峰峰值噪声。人们常常假定 RMS 与标准偏差相同,不过事实并非总是如此。这两个值只有在不存在 DC 元件(DC 元件为平均值 μ)的情况下才相同。就热噪声而言,由于没有DC 元件,因此标准偏差与 RMS 值相等。我们在附录中举出了“标准偏差与 RMS 相等”和“标准偏差与 RMS 不相等”两个不同的示例。
文章开头就给出了计算 RMS 热噪声电压的方程式。还有一种计算 RMS 噪声电压的方法就是先测量大量离散点,然后采用统计学方法估算标准偏差。举例来说,如果我们从模数 (A/D) 转换器中获得大量采样,那么我们就能运用方程式 1.4, 1.5 及 1.6 来计算噪声信号的平均偏差、标准偏差以及 RMS 值。附录中的示例 1.3 显示了在 Basic程序中如何运用上述方程式。我们在附录中还列出了一组更全面的统计方程供您参考。

方程式 1.4、1.5、1.6:离散数据的统计方程
本文最后要介绍的概念是噪声信号的叠加。为了叠加两个噪声信号,我们必须先了解信号是否相关。来自两个不同信号源的噪声信号彼此不相关。举例来说,来自两个不同电阻器或两个不同运算放大器的噪声是彼此不相关的。不过,噪声源通过反馈机制会产生关联。什么是相关噪声源叠加呢?一个很好的实例就是带噪声消除功能的耳机,其可通过累加反向相关的噪声来消除噪声。方程式 1.7 显示了如何叠加相关噪声信号。请注意,就带噪声消除功能的耳机而言,相关系数 C 应等于 - 1。

方程式 1.7: 叠加随机相关信号

方程式1.8: 叠加随机不相关的信号
在大多数情况下,我们都要叠加不相关的噪声源(见方程式 1.8)。在这种情况下叠加噪声,我们要通过勾股定理得到两个矢量噪声的和。图 1.5 显示了叠加噪声源的情况。我们通常可做近似地估计,如果一个噪声源强度为另一个的三分之一,较小的噪声源可忽略不计。
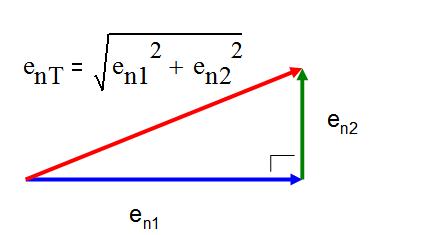
图 1.5: 噪声勾股定理
噪声包括固有噪声及外部噪声,这两种基本类型的噪声均会影响电子电路的性能。外部噪声来自外部噪声源,典型例子包括数字开关、60Hz 噪声以及电源开关等。固有噪声由电路元件本身生成,最常见的例子包括宽带噪声、热噪声以及闪烁噪声等。本系列文章将介绍如何通过计算来预测电路的固有噪声大小,如何采用 SPICE模拟技术,以及噪声测量技术等。
热噪声
热噪声由导体中电子的不规则运动而产生。由于运动会随温度的升高而加剧,因此热噪声的幅度会随温度的上升而提高。我们可将热噪声视为组件(如电阻器)电压的不规则变化。图 1.1 显示了标准示波器测得的一定时域中热噪声波形,我们从图中还可看到,如果从统计学的角度来分析随机信号的话,那么它可表现为高斯分布曲线。我们给出分布曲线的侧面图,从中可以看出它与时域信号之间的关系。

图 1.1: 在时间域中显示白噪声以及统计学分析结果
热噪声信号所包含的功率与温度及带宽直接成正比。请注意,我们可简单应用功率方程式来表达电压与电阻之间的关系 (见方程式1.1),根据该表达式,我们可以估算出电路均方根 (RMS) 噪声的大小。此外,它还说明了在低噪声电路中尽可能采用低电阻元件的重要性。

方程式 1.1:热电压
方程式 1.1 中有一点值得重视的是,根据该表达式我们还可计算出 RMS 噪声电压。在大多数情况下,工程师希望了解“最差条件下噪声会有多严重?”换言之,他们非常关心峰峰值电压的情况。如果我们要将 RMS 热噪声电压转化为峰峰值噪声的话,那么必须记住的一点是:噪声会表现为高斯分布曲线。这里有一些单凭经验的方法即根据统计学上的关系,我们可将 RMS 热噪声电压转化为峰峰值噪声。不过,在介绍有关方法前,我想先谈谈一些数学方面的基本原理。本文的重点在于介绍统计学方面的基本理论,随后几篇文章将讨论实际模拟电路的测量与分析事宜。
概率密度函数:
构成正态分布函数的数学方程式称作“概率密度函数”(见方程式 1.2)。根据一段时间内测得的噪声电压绘制出相应的柱状图,从该柱状图,我们可以大致看出函数所表达的形状。图 1.2 显示了测得的噪声柱状图,并给出了相应的概率密度函数。

方程式 1.2: 高斯曲线分布曲线对应的概率密度函数

图1.2: 根据相应的概率密度函数所绘制的分布曲线
概率分布函数:
概率分布函数是概率密度函数的积分。根据该函数,我们可了解某事件在给定的时间段内发生的概率(见方程式 1.3 与图 1.3)。举例来说,我们可以假定图 1.4 为噪声概率分布函数,该函数告诉我们,在任意时间点上,在 -1V 与 +1V 之间(即 (-1, 1) 区间内)检测到噪声电压的概率为 30%。

方程式 1.3: 概率分布函数

图 1.3: 概率密度函数与概率分布函数
概率分布函数对我们将RMS热噪声电压转化为峰峰值噪声非常有用。请注意,高斯分布曲线的尾部是无限延伸的,这就是说,任何噪声电压都是可能的。尽管理论上确实如此,但就实际情况而言,极大的瞬时噪声电压发生的可能性不大。举例来说,我们检测到噪声电压在 -3σ 与 +3σ 之间的概率为 99.7 %。换言之,噪声电压超出该范围的概率仅有0.3 %。因此,我们通常将噪声信号的峰值估算为±3σ(即 6σ)。请注意,也有些工程师将噪声的峰值估算为 6.6σ。人们对到底如何估计这个数值没有定论。图 1.4 显示,68% 的噪声都会不超过 2σ。表 1.1 总结了测量噪声电压时标准偏差与概率之间的关系。

图 1.4: 标准偏差与峰值噪声间的关系

表 1.1: 标准偏差数与测量概率百分比
因此,在一定的标准偏差条件下,我们可以根据关系式来估算峰值对峰值噪声。不过,总体来说,我们还是希望将 RMS 噪声电压转化为峰峰值噪声。人们常常假定 RMS 与标准偏差相同,不过事实并非总是如此。这两个值只有在不存在 DC 元件(DC 元件为平均值 μ)的情况下才相同。就热噪声而言,由于没有DC 元件,因此标准偏差与 RMS 值相等。我们在附录中举出了“标准偏差与 RMS 相等”和“标准偏差与 RMS 不相等”两个不同的示例。
文章开头就给出了计算 RMS 热噪声电压的方程式。还有一种计算 RMS 噪声电压的方法就是先测量大量离散点,然后采用统计学方法估算标准偏差。举例来说,如果我们从模数 (A/D) 转换器中获得大量采样,那么我们就能运用方程式 1.4, 1.5 及 1.6 来计算噪声信号的平均偏差、标准偏差以及 RMS 值。附录中的示例 1.3 显示了在 Basic程序中如何运用上述方程式。我们在附录中还列出了一组更全面的统计方程供您参考。

方程式 1.4、1.5、1.6:离散数据的统计方程
本文最后要介绍的概念是噪声信号的叠加。为了叠加两个噪声信号,我们必须先了解信号是否相关。来自两个不同信号源的噪声信号彼此不相关。举例来说,来自两个不同电阻器或两个不同运算放大器的噪声是彼此不相关的。不过,噪声源通过反馈机制会产生关联。什么是相关噪声源叠加呢?一个很好的实例就是带噪声消除功能的耳机,其可通过累加反向相关的噪声来消除噪声。方程式 1.7 显示了如何叠加相关噪声信号。请注意,就带噪声消除功能的耳机而言,相关系数 C 应等于 - 1。

方程式 1.7: 叠加随机相关信号

方程式1.8: 叠加随机不相关的信号
在大多数情况下,我们都要叠加不相关的噪声源(见方程式 1.8)。在这种情况下叠加噪声,我们要通过勾股定理得到两个矢量噪声的和。图 1.5 显示了叠加噪声源的情况。我们通常可做近似地估计,如果一个噪声源强度为另一个的三分之一,较小的噪声源可忽略不计。

图 1.5: 噪声勾股定理
