关于信号调制的工作原理
时间:04-11
来源:互联网
点击:
FCC通信频段
FCC 和其他国际组织一致认为,如果任由任何人随意使用任何频率,那么必然会导致绝对的混乱。因此,应为不同用户分配不同的频率范围。例如分别为 FM 无线电、AM 无线电、WiFi、移动电话、海事通信、空中交通管制、业余无线电、对讲机、军事通信、警用电台等应用分配不同频段。对了,我们还没提卫星或空间通信!这真是太乱了,幸亏有 FCC 帮助管理。如果您感到好奇,不妨用谷歌搜索一下,马上就能找到一个更详细的图表。
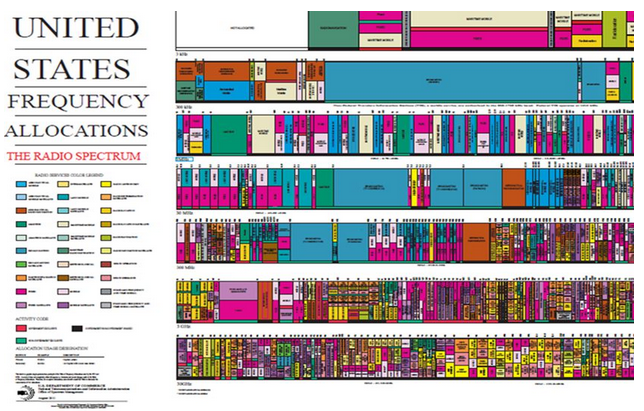
FCC 频谱分配表
FCC 已为小范围的个人应用、业余爱好者的应用和其他常规“ISM 频段”应用(工业、科学、医疗)预留了部分频段。这就是 WiFi、对讲机、无线传感器和其他通信设备的工作频段。让我们再次讨论一下频率!人耳的听力范围为 20Hz 至 20kHz。如果我们的 AM 电台为 680kHz,那么无线电塔如何将声音变到该频率呢?它如何避免干扰到其他电台?接收机如何将信号频率转换回可听范围?
调制
让我们离开频域,回到时域。再次重申一下:我们的讨论过于简单,略过了很多细节!在此只是为了得到一个概念性的结果。之所以这么说是因为,数学表示最适合在时域中使用,而图形表示在频域中效果最佳。
调制的作用就是将信号从低频(信息)转换到高频(载波)。思路很简单:用您的信息乘以高频载波,例如 680 kHz,这就是 AM 广播!稍等一下,事情果真如此简单吗?让我们看几个数学关系式。在此例中,θ 就是信息(可听内容),φ 是载波(例如, AM 广播频率)。
图中文字中英对照
Product-to-sum[23]
cos
sin
积化和差[23]
cos
sin
我们的 AM 信号如果用公式来表达,涉及多个信号的乘法运算,这在时域或频域中是很难想像的,因为我们仅仅看到音频是什么样的。但是上述这种对应关系告诉我们:两个信号相乘可用两个信号相加来表示!现在,我们很容易在频域中绘制出经乘法运算得到的信号。
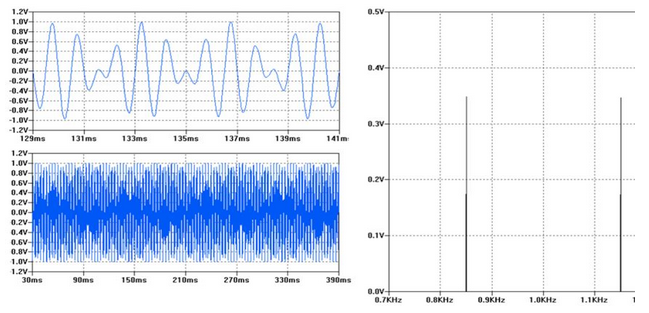
在载波(1000 Hz)上调制的单音频(150 Hz)
在此图中,我们用 150Hz 音频乘以 1000Hz 载波。上表显示了两个半功率信号,分别位于 1000-150 和 1000+150 Hz处,也就是在 850Hz 和 1150Hz 处。那么当经过调制后,我们每个音节的表现如何呢?
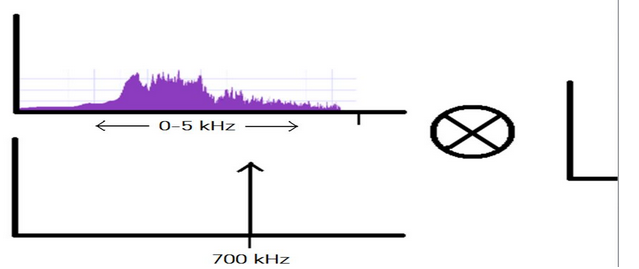
声音调制到 700 kHz
不出所料,我们看到了两个信号。一个是载波 + 信息,另一个是载波 - 信息(甚至注意到它是如何反转的)。
这就是 AM 频谱和信号内容的大致图解。

解调
现在我们来讨论接收机。所有信号均从天线开始,在同一时间查看所有信号,看到的是一团乱麻。天线拾取到大量的数据,但它并不负责进行分类,这是调谐器和其他硬件的工作。信号解调的原理与调制原理完全相同,非常方便!要将我们的音频信号转回到“基带”,并将其发送至扬声器,我们可以再次用载波乘以所有信号。
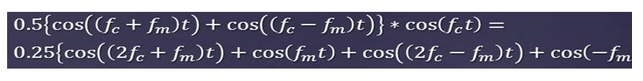
这个公式中包含一大串数学函数、括号和频率变量。不过它是对的,我们由此导出了四个信号:
1/4 功率信号,(2*载波 + 信息) 1/4 功率信号,(信息) 1/4 功率信号,(2*载波 - 信息) 1/4 功率信号,(-信息)
让我们忽略这个包含负频率的项,它是我们讨论调制及涉及的运算时,常常会出现的数学产物。在双倍载波上的两个信号(假设载波远大于信息,它们几乎是相同的)可用低通滤波器滤出。低通滤波器会阻断信号的所有高频内容,于是只将原始信息留给我们。我们可用放大器放大原始信息,然后发送到扬声器。太酷了!这就是它的图像,但是要向后延迟一点。
FCC 和其他国际组织一致认为,如果任由任何人随意使用任何频率,那么必然会导致绝对的混乱。因此,应为不同用户分配不同的频率范围。例如分别为 FM 无线电、AM 无线电、WiFi、移动电话、海事通信、空中交通管制、业余无线电、对讲机、军事通信、警用电台等应用分配不同频段。对了,我们还没提卫星或空间通信!这真是太乱了,幸亏有 FCC 帮助管理。如果您感到好奇,不妨用谷歌搜索一下,马上就能找到一个更详细的图表。

FCC 频谱分配表
FCC 已为小范围的个人应用、业余爱好者的应用和其他常规“ISM 频段”应用(工业、科学、医疗)预留了部分频段。这就是 WiFi、对讲机、无线传感器和其他通信设备的工作频段。让我们再次讨论一下频率!人耳的听力范围为 20Hz 至 20kHz。如果我们的 AM 电台为 680kHz,那么无线电塔如何将声音变到该频率呢?它如何避免干扰到其他电台?接收机如何将信号频率转换回可听范围?
调制
让我们离开频域,回到时域。再次重申一下:我们的讨论过于简单,略过了很多细节!在此只是为了得到一个概念性的结果。之所以这么说是因为,数学表示最适合在时域中使用,而图形表示在频域中效果最佳。
调制的作用就是将信号从低频(信息)转换到高频(载波)。思路很简单:用您的信息乘以高频载波,例如 680 kHz,这就是 AM 广播!稍等一下,事情果真如此简单吗?让我们看几个数学关系式。在此例中,θ 就是信息(可听内容),φ 是载波(例如, AM 广播频率)。
图中文字中英对照
Product-to-sum[23]
cos
sin
积化和差[23]
cos
sin
我们的 AM 信号如果用公式来表达,涉及多个信号的乘法运算,这在时域或频域中是很难想像的,因为我们仅仅看到音频是什么样的。但是上述这种对应关系告诉我们:两个信号相乘可用两个信号相加来表示!现在,我们很容易在频域中绘制出经乘法运算得到的信号。

在载波(1000 Hz)上调制的单音频(150 Hz)
在此图中,我们用 150Hz 音频乘以 1000Hz 载波。上表显示了两个半功率信号,分别位于 1000-150 和 1000+150 Hz处,也就是在 850Hz 和 1150Hz 处。那么当经过调制后,我们每个音节的表现如何呢?

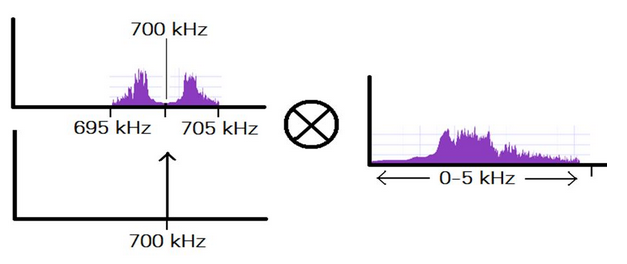
声音调制到 700 kHz
不出所料,我们看到了两个信号。一个是载波 + 信息,另一个是载波 - 信息(甚至注意到它是如何反转的)。
这就是 AM 频谱和信号内容的大致图解。

解调
现在我们来讨论接收机。所有信号均从天线开始,在同一时间查看所有信号,看到的是一团乱麻。天线拾取到大量的数据,但它并不负责进行分类,这是调谐器和其他硬件的工作。信号解调的原理与调制原理完全相同,非常方便!要将我们的音频信号转回到“基带”,并将其发送至扬声器,我们可以再次用载波乘以所有信号。
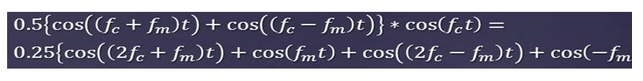
这个公式中包含一大串数学函数、括号和频率变量。不过它是对的,我们由此导出了四个信号:
1/4 功率信号,(2*载波 + 信息) 1/4 功率信号,(信息) 1/4 功率信号,(2*载波 - 信息) 1/4 功率信号,(-信息)
让我们忽略这个包含负频率的项,它是我们讨论调制及涉及的运算时,常常会出现的数学产物。在双倍载波上的两个信号(假设载波远大于信息,它们几乎是相同的)可用低通滤波器滤出。低通滤波器会阻断信号的所有高频内容,于是只将原始信息留给我们。我们可用放大器放大原始信息,然后发送到扬声器。太酷了!这就是它的图像,但是要向后延迟一点。

无线电 滤波器 放大器 电子 电压 低通滤波器 传感器 相关文章:
- 软件无线电的电磁兼容分析(02-26)
- 对信息技术设备的无线电骚扰管理方法的研究(02-27)
- 雷达信号及其监测研究(03-02)
- 基于认知无线电技术的IEEE 802.22(10-02)
- 4G移动通信关键技术及特征(03-09)
- 无线电频率资源的合理配置(08-16)
