UWB的无线传感器网络的定位技术
时间:10-18
来源:互联网
点击:
在很多无线传感器网络(WSN)应用中,没有节点位置信息的监测往往毫无意义。当监测到事件发生时,关心的一个重要问题就是该事件发生的位置,如森林火灾监测,天然气管道泄漏监测等。这些事件的发生,首先需要知道的就是自身的地理位置信息。定位信息除了用来报告事件发生的地点外,还可用于目标跟踪、目标轨迹预测、协助路由以及网络拓扑管理等。因此节点定位问题已成为无线传感器网络的一个首要解决的问题。
1 问题描述
超宽带(Ultra WideBanol,UWB)通信技术是一种以ns级的冲击脉冲在短距离内高速传输数据的无线通信技术。这种通信技术具有隐蔽性好、穿透能力强、定位精度高以及功耗低等特点,在无线传感器网络的测距、定位应用中,具有十分重要的现实作用,并己经应用到实际物资供应跟踪定位中。
UWB信号具有非常宽的带宽,将其应用于TOA定位方法有助于实现较高的测距精度。然而,在实际应用环境常常出现多径干扰,此时UWB直达信号难以精确检测。因而,本文提出了通过模糊逻辑技术对首次到达信号时间和最强信号时间进行加权来得到直达信号到达时间的方法,使得UWB在无线传感器网络节点定位中的应用成为可能。
2 TOA距离估计方法
对于一个单路径加性白噪声(Additive White Gaussian Noise,AwGN)信道条件,可以利用TOA测距的距离估计根均方差:
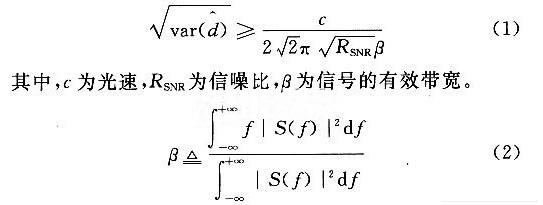
其中,S(f)为发送的传输信号的傅立叶变换。显然,估计的根均方差同信号的RSNR和有效带宽有关,RSNR和有效带宽越大,估计的根均方差越小。由于UWB信号带宽非常宽,UWB无线信号应用基于时间的技术可实现相对精确的定位。
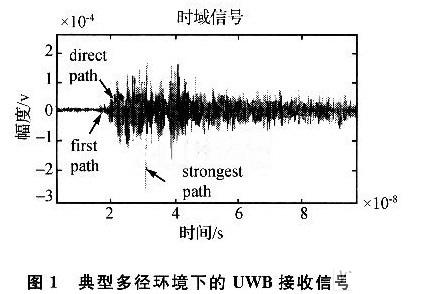
一般情况下,TOA定位方法是利用检测接收信号中的直达路径的到达时间,来测量通信收发节点间的距离。因此,对直达路径信号到达时间的精确估计是至关重要的。本文所讨论的节点定位方法针对的是典型的无线传感器网络。一般来说,通过检测接收到信号的幅度是否最大来确定直达信号的到达时间,但是这种方法在多径条件下难以达到较高的测量精度。典型多径环境下的UWB接收信号如图1所示。直达信号(direct path)并非首次到达信号(first path,与门限有关)或幅度最强信号(strongest path),因此在这种情况下,使用首次到达信号或幅度最强信号的到达时间都不能准确估计发射端节点和接收端节点之间的距离。可以利用最大似然估计法检测直达路径信号的到达时间来计算传感器节点之间的距离,但在复杂多径环境下容易造成信号波形的失真,因此有一定的实现难度。针对UWB直达信号难以精确检测的特点,本文提出通过对首次到达信号时间和最强信号时间进行加权来得到直达信号到达时间,其加权系数由模糊逻辑技术获得。
3 基于模糊逻辑的权值选取
设UWB信号在T0时刻被发送,在接收端节点接收到的首次到达信号和幅度最强信号的到达时刻分别为Tf和Ts,而直达信号到达时刻通过下式计算:

其中c=3×108m/s,为无线电信号在自由空间的传播速度。
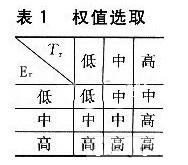
这里使用模糊逻辑技术来选取权值a。设首次到达信号和幅度最强信号的幅度分别为Ef和Es,并定义E=|Ef|/|Es|,Tr=(Tf- T0)/(Ts-T0)。Er和Tr为模糊逻辑函数的输入,a为输出。Er、Tr和a分别定义了低、中、高3个值。选择a值的规则如表1所列。
4 仿真分析
对测得的多径环境下的UWB接收信号方法的测距精度进行验证,并结合节点定位技术,对节点进行定位。Er,Tr和a的隶属函数如图2所示。
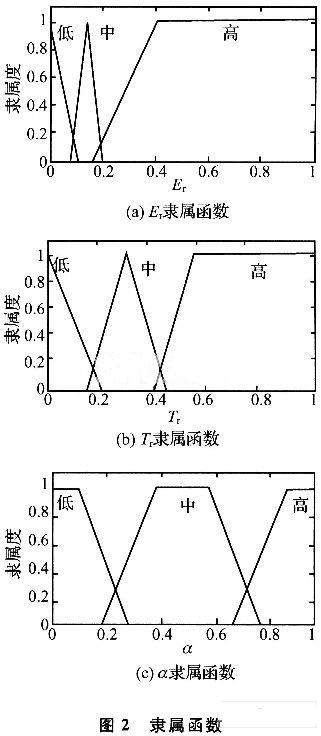
取发射信号时刻T0=0,在接收端分别记录下首次到达信号时刻Tf,幅度最强信号的到达时刻Ts,首次到达信号幅度Ef和幅度最强信号的幅度 Es。分别计算出模糊逻辑的输入值Er、Ts,根据隶属函数,可以得到a。将Tf、Ts、a代入(3)式即可得到直达信号到达时刻T,进而结合(4)式计算出两点之间的距离。
假设有三个参考节点(0,0)、(10,0)、(10,10),盲节点到参考节点的实际距离分别为6.20、2.88、9.46,利用三边测量法可以获得节点的位置,如表2所列。
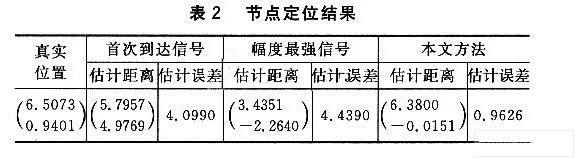
这里,定义节点定位误差为节点的真实位置与估计位置的欧几里得距离。从表中可以看出,在节点定位中,应用基于UWB的测距技术可极大地提高节点定位精度。
1 问题描述
超宽带(Ultra WideBanol,UWB)通信技术是一种以ns级的冲击脉冲在短距离内高速传输数据的无线通信技术。这种通信技术具有隐蔽性好、穿透能力强、定位精度高以及功耗低等特点,在无线传感器网络的测距、定位应用中,具有十分重要的现实作用,并己经应用到实际物资供应跟踪定位中。
UWB信号具有非常宽的带宽,将其应用于TOA定位方法有助于实现较高的测距精度。然而,在实际应用环境常常出现多径干扰,此时UWB直达信号难以精确检测。因而,本文提出了通过模糊逻辑技术对首次到达信号时间和最强信号时间进行加权来得到直达信号到达时间的方法,使得UWB在无线传感器网络节点定位中的应用成为可能。
2 TOA距离估计方法
对于一个单路径加性白噪声(Additive White Gaussian Noise,AwGN)信道条件,可以利用TOA测距的距离估计根均方差:
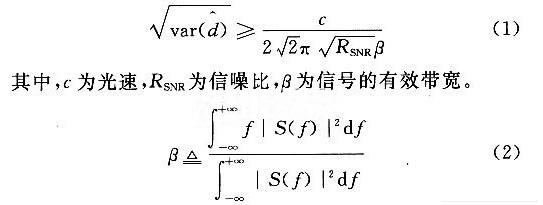
其中,S(f)为发送的传输信号的傅立叶变换。显然,估计的根均方差同信号的RSNR和有效带宽有关,RSNR和有效带宽越大,估计的根均方差越小。由于UWB信号带宽非常宽,UWB无线信号应用基于时间的技术可实现相对精确的定位。
一般情况下,TOA定位方法是利用检测接收信号中的直达路径的到达时间,来测量通信收发节点间的距离。因此,对直达路径信号到达时间的精确估计是至关重要的。本文所讨论的节点定位方法针对的是典型的无线传感器网络。一般来说,通过检测接收到信号的幅度是否最大来确定直达信号的到达时间,但是这种方法在多径条件下难以达到较高的测量精度。典型多径环境下的UWB接收信号如图1所示。直达信号(direct path)并非首次到达信号(first path,与门限有关)或幅度最强信号(strongest path),因此在这种情况下,使用首次到达信号或幅度最强信号的到达时间都不能准确估计发射端节点和接收端节点之间的距离。可以利用最大似然估计法检测直达路径信号的到达时间来计算传感器节点之间的距离,但在复杂多径环境下容易造成信号波形的失真,因此有一定的实现难度。针对UWB直达信号难以精确检测的特点,本文提出通过对首次到达信号时间和最强信号时间进行加权来得到直达信号到达时间,其加权系数由模糊逻辑技术获得。

3 基于模糊逻辑的权值选取
设UWB信号在T0时刻被发送,在接收端节点接收到的首次到达信号和幅度最强信号的到达时刻分别为Tf和Ts,而直达信号到达时刻通过下式计算:

其中c=3×108m/s,为无线电信号在自由空间的传播速度。
这里使用模糊逻辑技术来选取权值a。设首次到达信号和幅度最强信号的幅度分别为Ef和Es,并定义E=|Ef|/|Es|,Tr=(Tf- T0)/(Ts-T0)。Er和Tr为模糊逻辑函数的输入,a为输出。Er、Tr和a分别定义了低、中、高3个值。选择a值的规则如表1所列。

4 仿真分析
对测得的多径环境下的UWB接收信号方法的测距精度进行验证,并结合节点定位技术,对节点进行定位。Er,Tr和a的隶属函数如图2所示。

取发射信号时刻T0=0,在接收端分别记录下首次到达信号时刻Tf,幅度最强信号的到达时刻Ts,首次到达信号幅度Ef和幅度最强信号的幅度 Es。分别计算出模糊逻辑的输入值Er、Ts,根据隶属函数,可以得到a。将Tf、Ts、a代入(3)式即可得到直达信号到达时刻T,进而结合(4)式计算出两点之间的距离。
假设有三个参考节点(0,0)、(10,0)、(10,10),盲节点到参考节点的实际距离分别为6.20、2.88、9.46,利用三边测量法可以获得节点的位置,如表2所列。

这里,定义节点定位误差为节点的真实位置与估计位置的欧几里得距离。从表中可以看出,在节点定位中,应用基于UWB的测距技术可极大地提高节点定位精度。
- 光缆结构及工艺的发展(03-04)
- 基于Zigbee的远程家庭监护系统的应用研究(04-08)
- 触摸屏基本原理(04-16)
- 无线传感器网络的服务质量保障技术(10-16)
- 网络自组织通信模式和技术研究综述(10-26)
- 视频传感器网络覆盖控制(Coverage Control)问题研究概述(11-24)
