T-S-T三级交换网络路径搜索算法的研究

6 算法的正确性证明和复杂度分析

从前面的分析可以知道，要解决整个交换算法的关键是确定和寻找中间矩阵after_s，也就是说，在解决问题之前，必须确定问题有解。如何确定after_s一定存在，这里可以通过组合数学中的抽屉原理证明必然存在这样的矩阵，证明过程比较简单，本文在这里不做推导证明。

从前面的理论分析中知道，衡量交换算法有2个重要的指标：交换次数和比较次数。为了统计本文所研究的交换算法的性能，本文针对不同阶数矩阵的交换次数和比较次数做了系统的统计：

(1)对于每一行数据，由于统计冲突值、判回溯算法和元素的安放算法都是多项式复杂度，所以，在不存在回溯的条件下，本算法是多项式复杂度。

(2)在本算法中，“冲突”起着非常重要的作用，本身回避了许多回溯可能。即使回溯，本行可供回溯元素和非回溯元素“待”的位置个数非常有限，所以元素回溯的空间很小。

下面本文给出在不回溯的情况下，对高冲突行优先排列算法在阶数递增变化时，50次平均交换次数和比较次数统计结果如表1所示。



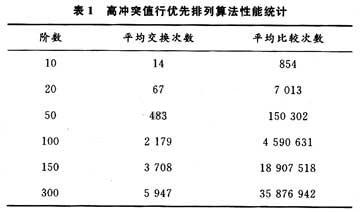
从前面对该算法的描述可知，该算法通过使每个元素“找到”尽可能适合自己的位置，从而回避了重新排列的许多可能，对于一行来说，完全避免了全排列，而且大大减小回溯概率。由于对大多数(约80％)矩阵来说，是不会出现回溯的，只有类似这样的矩阵才有可能出现回溯(也可能不回溯)，即，AS的某些行，可供选择的初始行太少。所以，该算法是一个近似多项式的算法，在不回溯的情况下，是多项式算法。该算法基本上能够完成交换网络的路径接续，他有一个很大的优势就是在交换过程中交换的次数达到最小，这样也就大大提高了寻找交换路径的效率。本算法具有良好的特性，而且通过芯片级联可实现。