一种新颖的天线小型化技术及其应用

1 引言   

近年来，无线通信技术以惊人的速度发展，无论用户身在何处都能够时刻处于连接状态，这就是所说的"任何时间、任何地点的无线电通信"。而天线和射频设备是决定整个系统性能的关键元件。由于传统的天线已经无法满足未来的挑战，这就意味着必须相应地发展天线技术以适应无线系统发展的要求。  

目前分形正成为满足未来产品要求的一种有效方法。他能够使得我们有效地设计小型化天线或把多个无线电通信元件集成到一块设备上。
在用于无线应用中的下一代天线中，小型化是必须的。因为他必须集成多个设备(如蜂窝、无线局域网、地理定位、无线电广播装置)，并需要安置在多个地点＜如机场、办公室、商场、地下场所)，同时很多设备也需用到小型化天线，如手机、笔记本电脑、个人数字助理、汽车、手表等。在这种情况下，用户希望采用尽可能小的天线以便于方便使用无线设备。此外，在基站和设备的接人点处，小型化的夭线有助于
减少周围环境对无线网络设施的影响。  

2 分形几何背景知识  

"分形"这一概念是由法国数学家B.Mandelbrot于1975年首次提出的，"分形(Fractal)"这个名词源于拉丁文的"破碎"。分形具有两大主要特征：自相似性和空间填充性(即分数维)。  

自相似 就是说适当的放大或缩小几何尺寸，整个结构并不改变，在各种尺度上都有相同程度的不规则性。 分数维 是指用一个特征数(不一定是整数)来测定其不平度、复杂性或卷积度。  

自然界中的许多物体都能用分形来模拟，如山脉、树木和云彩等如图1所示。  

  

分形技术是得益于数学上分形物体的一些特殊性质发展起来的。无论是自然界中的分形还是数学上的分形物体，都能够通过简单的算法一步步迭代生成，最终能够具有惊人的复杂结构。分形的特性之一就是"分数维"。这种特性使得分形能够在很小的体积内充分的利用空间，也是他能够用于天线小型化设计的一个关键原因。  

2．1 分形曲线生成过程举例  

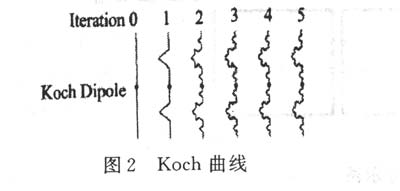
以Koch曲线的生成方法为例，把一条直线等分为三段，将中间的一段用具有一定夹角的两条等长折线来代替，形成一个生成元，然后再把每个直线段用生成元进行替换，经多次迭代后就形成了Koch曲线(如图2所示)。由此可见，在保持高度基本不变时，曲线的长度却能够做到无限长。  

2．2 分形几何与欧氏几何的区别  

欧氏几何的基本元素是点、线、薄片和体积，而分形几何没有这么具体、清晰的概念，如：分形中的一条线可能接近于一个薄片。在这种方式下，一条分形线能够很好的填充一个薄片。这种空间填充特性使得曲线长度很长，又合适于紧凑的物理空间。这种性质十分适用于天线的小型化设计。  



3 几种经典的分形天线  

3．1 Koch单极天线  

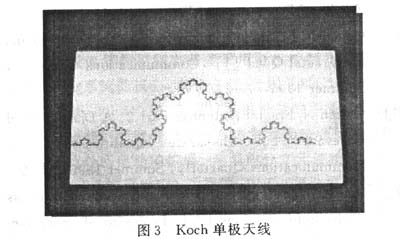
分形用于天线小型化设计的第一个例子是Koch单极天线(如图3所示)，得名于分形Koch曲线。当在天线的设计中应用Koch曲线时，谐振频率相对于传统的线性单极天线以1．65的因数降低。所以Koch单极天线的高度比传统的线性单极天线小40％"。   


3．2 Hilbert分形天线  

另一个已实际应用于天线小型化设计的例子是Hilbert分形天线(如图4所示)。由于是由多节线段组成的，Hilben曲线是一种比传统的曲线能够覆盖更多的空间的分形曲线，其生成过程如图5所示。事实上，他几乎可以看作一系列的点来填满整个的正方形表面(本身仍保持是条曲线)。利用这种特性，许多天线的尺寸都可以大大减小。  



  

目前，这种分形天线多用于VHF和UHF。  

3．3 分形环天线  

欧氏几何中的环天线有一定的局限性：谐振环要求巨大的空间，小环的输入阻抗很低等。而分形环天线与之相比有如下优势：  

(1)天线小型化。在占用空间相同的情况下分形环能够使天线环的周长为无限长:在频率较低时，天线可以在很小的空间内利用分形曲线实现。

(2)使得天线的辐射阻抗增加。

(3)分形环天线具有更强的方向性。

目前的分形环天线主要有Koch分形环、Minkowski分形环等，如图6所示。  

  

3.4 分形天线阵列  

分形几何应用于天线阵列的设计主要有两种方式，分形单元可用于均匀分布阵列中，也可以将阵列间距用分形形式来布局。分形阵列与传统的阵列设计相比有如下特点：  

(1)多频、宽频特性。

(2)可用迭代算法快速计算方向图。

(3)可系统的稀疏阵列。

(4)可有效地设计大的平面阵列。

(5)可实现低副瓣设计策略。

目前两种典型的分形阵列天线是Cabtor集阵列和Weierstrass线性阵列。