低通模拟滤波器的设计方案

　　几乎所有电子电路中都能看到有源模拟滤波器的身影。音频系统使用滤波器进行频带限制和平衡。通信系统设计师使用滤波器调谐特定频率并消除其它频率。为了使高频信号衰减，所有数据采集系统都在模数转换器（ADC）前面有一个抗锯齿（低通）滤波器，或者在数模转换器（DAC）后面有一个抗镜像（低通）滤波器。这种模拟滤波还可以在信号到达ADC之前或者离开DAC之后，消除叠加在信号上面的高频噪声。如果ADC的输入信号超出转换器采样频率的一半，则该信号的大小被可靠地转换；但是，在其变回数字输出时，频率也发生改变。

　　利用TI的WEBENCH 滤波器设计器软件，可以高效地设计出低通、高通、带通或者带阻滤波器。这种应用程序替代了TI的FiLTErPro 和以前国家半导体的WEBENCH有源滤波器设计器软件。在生成有源滤波器时，它使用这些程序和公式。但是，它允许深度调节各种滤波器变量，优化滤波器，为滤波器电路寻找到正确的TI运算放大器 （op amp），并具有SPICE模拟功能，比上面两个程序更加强大。

　　低通模拟滤波器的重要设计参数

　　低通模拟滤波器的频域规范包括4个基础参数：

　　fc，即滤波器的-3-dB截止频率

　　Ao，即滤波器的增益

　　Asb，即阻带衰减

　　fs，即阻带衰减的中断频率

　　图1所示WEBENCH滤波器设计器的滤波器类型窗口列出了这些参数。DC到截止频率（fc）的频率范围为带通区域。图1中Ao为带通响应量级。使用巴特沃兹（Butterworth）或者贝塞尔（Bessel）滤波器时，带通响应可以为扁平，并且无纹波。相反，一直到截止频率，切比雪夫（Chebyshev）滤波器都有纹波。切比雪夫滤波器的纹波误差量级为2△AMAX.

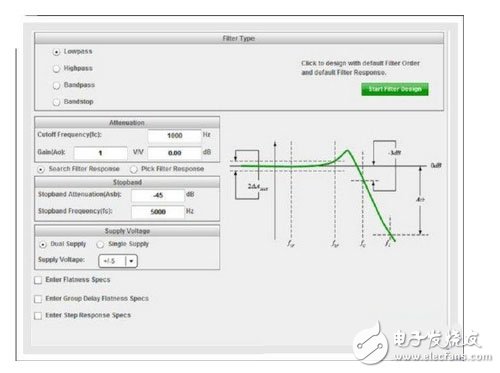
　　图1 WEBENCH 滤波器设计器重要模拟滤波器参数

　　滤波器响应超出fc时，它会通过过渡带降至阻带区域。滤波器近似法（巴特沃兹、贝塞尔和切比雪夫等）决定过渡带的带宽和滤波器的阶数（M）。传输函数的极点数决定滤波器阶数。例如，如果某个滤波器的传输函数内有3个极点，则其为一个三阶滤波器。

　　一般而言，当更多极点用于实现滤波器设计时过渡带变得更小，如图2巴特沃兹低通滤波器所示。理想情况下，低通、抗锯齿滤波器应有"砖墙"式响应，并且过渡带极小。实际而言，这并不是最好的抗锯齿方法。进行有源滤波器设计时，每两个极点就要求有一个运算放大器。例如，32阶滤波器要求16个运算放大器、32个电容器和多达48个电阻器。

　　
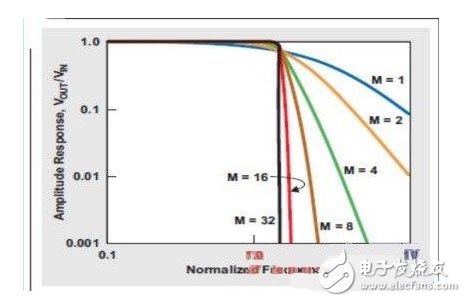
图2 巴特沃斯滤波器极点数增加带来更加明显的转降

　　模拟滤波器近似计算类型

　　图3显示了WEBENCH滤波器设计器观察屏幕的解决方案窗口中一些可用的低通滤波器类型。用户点击"开始滤波器设计"按钮（图1）以后，出现该屏幕。

　　　
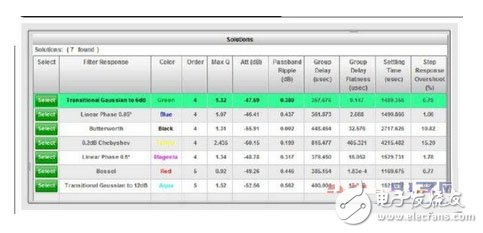
　图3 WEBENCH 滤波器设计器的低通滤波器类型

　　巴特沃兹、贝塞尔和切比雪夫是一些比较流行的滤波器近似法类型。查看量级和频率域对比以及量级和时域对比情况以后，可以知道滤波器类型。

　　巴特沃兹滤波器

　　巴特沃兹滤波器传输函数包括所有极点，并且没有零，其表达式如下：

　　图4表明四阶、低通巴特沃兹滤波器的响应在带通部分为扁平。这种特性的技术术语称作"最大扁平"。之后，它会显示，过渡带的衰减速率不如切比雪夫滤波器。

　　图5表明，相同四阶巴特沃兹滤波器的阶跃响应在时域中有一些过冲和振铃。如果滤波器阶数更高，则这种过冲也会更高。如果这种滤波器用在多路器之后，则应考虑其稳定时间。

　　　　
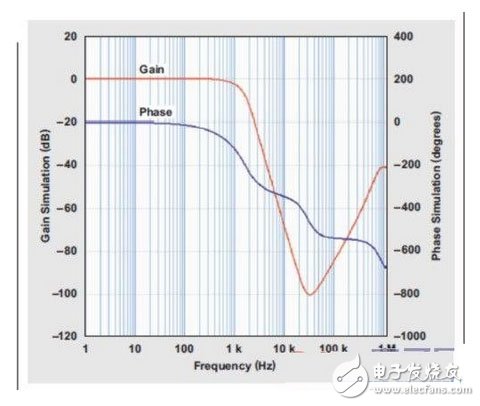
图4 四阶、低通巴特沃斯滤波器的频率响应

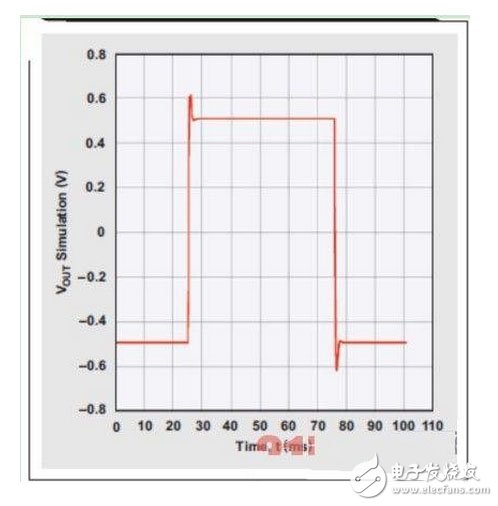
图5 四阶、低通巴特沃斯滤波器的阶跃响应

　　切比雪夫滤波器的传输函数与巴特沃兹滤波器类似，因为它具有所有极点，并且没有零：

　　图6表明，四阶、低通切比雪夫滤波器的频率响应在带通区域有0.2dB的纹波。电路设计的极点布局决定了这种纹波。总之，纹波量级的增加会降低过渡带的宽度。

　　理论上，2△AMAX（图1）的纹波量级可以如我们预期的那样大或者小。高纹波量级一般会带来更多的带通区域误差，但却可以实现更快的过渡带衰减。

　　相比巴特沃兹滤波器，过渡带衰减速率变化更剧烈。例如，为了满足0.5dB纹波的三阶切比雪夫滤波器的过渡带宽要求，要求使用一个四阶巴特沃兹滤波器。尽管使用切比雪夫滤波器时在带通区域存在振铃，但阻带没有振铃。

　　0.2dB纹波的四阶、低通切比雪夫滤波器的阶跃响应，存在相当程度的过冲和振铃（图7）。

　　　　
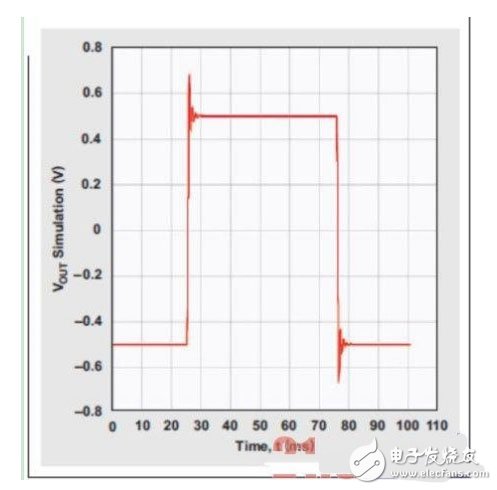
图7 四阶、低通切比雪夫滤波器的阶跃响应

过冲和振铃现象是频域中相位响应的结果。我们都还记得，阶跃响应（或者方波）傅立叶分析表明，通过增加奇数谐波正弦信号可以建立方波。结果是