合理选择电容器来实现高性能的EMI滤波

　　本文将重点讨论多层陶瓷电容器，包括表面贴装和引脚两种类型。讨论如何计算这些简单器件的阻抗和插入损耗之间的相互关系。文中还介绍了一些改进型规格的测试，如引线电感和低频电感，另外，还给出了等效电路模型。这些模型都是根据测得的数据导出的，还介绍了相关的测试技术。针对不同的制造工艺，测试了这些寄生参数，并绘制出了相应的阻抗曲线。

　　长期以来，一直使用旁路和去耦电容来减小PCB上产生的各种噪声，也。由于成本相对较低，使用容易，还有一系列的量值可选用，电容器常常是电路板上用来减小电磁干扰（EMI）的主要器件。由于寄生参数具有重要的影响，故电容器的选择要比其容量的选择更为重要。制造电容器的方法很多，制造工艺决定了寄生参数的大小。

　　电气器噪声可以以许多不同的方式引起。在数字电路中，这些噪声主要由开关式集成电路，电源和调整器所产生，而在射频电路中则主要由振荡器以及放大电路产生。无论是电源和地平面上，还是信号线自身上的这些干扰都将会对系统的工作形成影响，另外还会产生辐射。

　　本文将重点讨论多层陶瓷电容器，包括表面贴装和引脚两种类型。讨论如何计算这些简单器件的阻抗和插入损耗之间的相互关系。文中还介绍了一些改进型规格的测试，如引线电感和低频电感，另外，还给出了等效电路模型。这些模型都是根据测得的数据导出的，还介绍了相关的测试技术。针对不同的制造工艺，测试了这些寄生参数，并绘制出了相应的阻抗曲线。

　　阻抗和插入损耗

　　所幸的是，电容器还算简单的器件。由于电容器是一个双端口器件，故仅有一种方法与传输线并接。不要将该器件看作一只电容器，更容易的方法是将其看作为一个阻抗模块。当其与传输线并联时，甚至可以将其视作为一个导纳模块（见图1）。

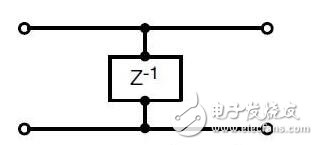
　　图1：将电容器视作为阻抗模块。

　　这种连接方式的ABCD参数可以表示为：

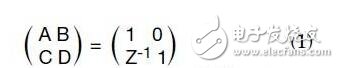
　　然后，利用ABCD参数和散射（S）参数之间的关系，可以得到插入损耗S21的幅度为：

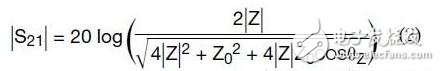
　　式中，Z=阻抗幅度

　　Z0=传输线阻抗

　　有一些插入点可以来观察方程2。首先，对于一个高性能的陶瓷电容器来说，其相角在整个频段中都非常接近±90°，只有谐振点附近除外（见图2）。

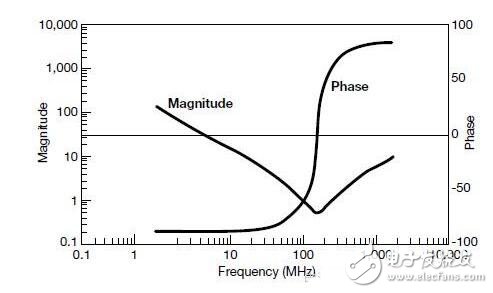
　　图2：1000-pF陶瓷电容器的典型阻抗幅相特性。

　　已知±90°的余弦接近0，故方程2可以被简化为：

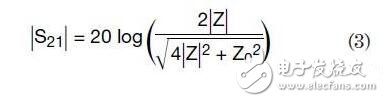
　　故该相角可以被忽略，并且在绝大多数的频谱上都能给出较好的结果。另一个很好的近似是当Z0》》？Z？？时，方程3可以被进一步简化为：

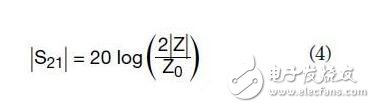
　　作为一个例子，表1中给出了对一只1000-pF的旁路电容器测出的阻抗及由此计算出来的插入损耗。所有的插入损耗数据都基于50欧阻抗。如表中所给出，一旦电容器的阻抗开始增加到50欧，方程3将快速发生突变。

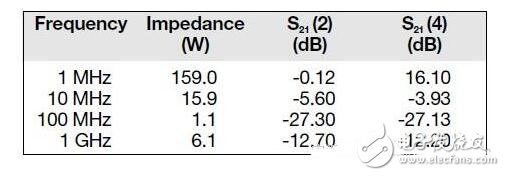
　　表1：1000-pF旁路电容器的阻抗和求得的插入损耗。

　　这些方程中的唯一问题就是需要知道一系列不同电容值的阻抗。

　　多层陶瓷电容器（MLCC）串联模型

　　对于MLCC电容器来说，最简单的（当然也是最有效的）模型是串联模型（见图3）。

　　图3：陶瓷电容器的等效串联模型。

　　该模型给出了适用于绝大多数表面贴装MLCC的正确阻抗曲线。记住电容值将随温度和直流偏置而变化。等效串联电阻（ESR）随温度、直流偏置和频率变化，而等效串联电感（ESL）却基本保持不变。对阻抗来说，也许最重要的部分是谐振点，因为这是衰减最大的频率。众所周知，计算谐振频率的公式是：

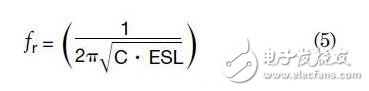
　　对于各类表面贴装的不同封装的电感值，可以利用方程2中所描述的测量技术来计算。例如，如果系统中产生了800MHz的噪声，随后可以在PCB上将其定位到一个确定的区域。选择一个标称容量为39pF的电容，并将其安装到尽可能靠近产生噪声的地方，这对于减小EMI来说，将是最好的选择。减小矩形芯片电感的一个有效方式就是改进芯片纵长方向端头的设计。所选电容器的阻抗曲线如图4所示。注意通过改变纵横比，寄生电感减小了大约50%，即从1200pH减小到600pH。这有效地偏移开了最大衰减点，故在利用这些器件来进行EMI滤波时只需牢记这一点。

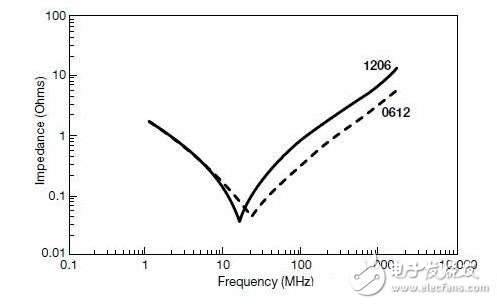
　　图4：两只0.1 μF电容器的阻抗曲线比较。

　　低电感电容的最大优点体现在数字电路退耦中。利用如下简单的电感方程：

　　利用低电感芯片来降低电感，可以减小集成电路中开关时所产生的总电压噪声。

　　引脚电容器

　　引脚电容相对于表面贴装电容器，除了增加了引脚之外，其他并没有什么不同。其等效模型与MLCC模型一样，除了增加了引脚所产生的电感之外，见图5。

　　图5：引脚电容器的等效模型

引脚所