分享一些最常见最实用的机器学习算法

pport Vector Machine，SVM）

SVM是二进制分类算法。给定N维坐标下两种类型的点，SVM生成（N-1）维的超平面来将这些点分成两组。假设你在平面上有两种类型的可以线性分离的点，SVM将找到一条直线，将这些点分成两种类型，并且这条直线尽可能远离所有这些点。

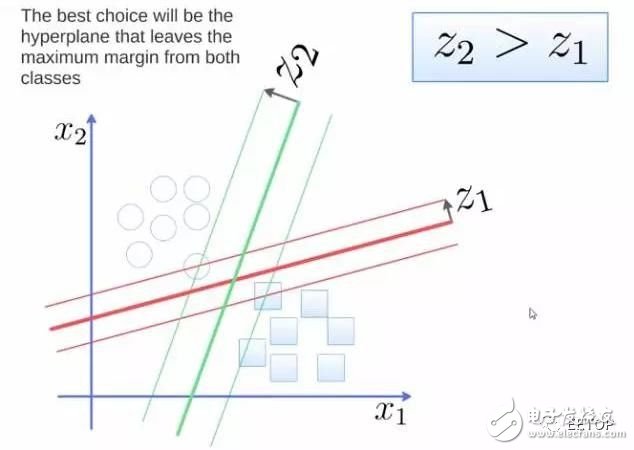
从规模上看，使用SVM（经过适当的修改）解决的一些最大的问题包括显示广告、人类剪切位点识别（human splice site recognition）、基于图像的性别检测，大规模图像分类……

SVM算法优点：

可用于线性/非线性分类，也可以用于回归；

低泛化误差；

容易解释；

计算复杂度较低；

缺点：

对参数和核函数的选择比较敏感；

原始的SVM只比较擅长处理二分类问题；

6.集成方法（Ensemble methods）

集成方法是学习算法，它通过构建一组分类器，然后通过它们的预测结果进行加权投票来对新的数据点进行分类。原始的集成方法是贝叶斯平均，但是最近的算法包括纠错输出编码、Bagging和Boosting。

那么集成方法如何工作？并且为什么它们要优于单个模型？

• 它们平均了单个模型的偏差：如果你将民主党的民意调查和共和党的民意调查在一起平均化，那么你将得到一个均衡的结果，不偏向任何一方。

• 它们减少了方差：一组模型的总体意见比其中任何一个模型的单一意见更加统一。在金融领域，这就是所谓的多元化，有许多股票的组合比一个单独的股票的不确定性更少，这也为什么你的模型在数据多的情况下会更好的原因。

• 它们不太可能过拟合：如果你有单个的模型没有过拟合，那么把这些模型的预测简单结合起来（平均、加权平均、逻辑回归），那么最后得到的模型也不会过拟合。

无监督学习

7.聚类算法（Clustering Algorithms）

聚类是将一系列对象分组的任务，目标是使相同组（集群）中的对象之间比其他组的对象更相似。

根据聚类思想划分：

1. 基于划分的聚类:

K-means, k-medoids(每一个类别中找一个样本点来代表),CLARANS.

k-means是使下面的表达式值最小：

k-means算法的优点：

（1）k-means算法是解决聚类问题的一种经典算法，算法简单、快速。

（2）对处理大数据集，该算法是相对可伸缩的和高效率的，因为它的复杂度大约是O(nkt)，其中n是所有对象的数目，k是簇的数目,t是迭代的次数。通常k

（3）算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的，且簇与簇之间区别明显时，聚类效果较好。

缺点：

（1）k-平均方法只有在簇的平均值被定义的情况下才能使用，且对有些分类属性的数据不适合。

（2）要求用户必须事先给出要生成的簇的数目k。

（3）对初值敏感，对于不同的初始值，可能会导致不同的聚类结果。

（4）不适合于发现非凸面形状的簇，或者大小差别很大的簇。

（5）对于"噪声"和孤立点数据敏感，少量的该类数据能够对平均值产生极大影响。

2. 基于层次的聚类：

自底向上的凝聚方法，比如AGNES。

自上向下的分裂方法，比如DIANA。

3. 基于密度的聚类：

DBSACN,OPTICS,BIRCH(CF-Tree),CURE.

4. 基于网格的方法：

STING, WaveCluster.

5. 基于模型的聚类：

EM,SOM,COBWEB.

每一种聚类算法都不相同，下面是一些例子：

• 基于质心的算法

• 基于连接的算法

• 基于密度的算法

• 概率

• 降维

• 神经网络/深度学习

8.主成分分析（Principal Component Analysis，PCA）

PCA是一个统计学过程，它通过使用正交变换将一组可能存在相关性的变量的观测值转换为一组线性不相关的变量的值，转换后的变量就是所谓的主分量。

PCA的一些应用包括压缩、简化数据便于学习、可视化等。请注意，领域知识在选择是否继续使用PCA时非常重要。 数据嘈杂的情况（PCA的所有成分具有很高的方差）并不适用。

9.奇异值分解（Singular Value Decomposition，SVD）

在线性代数中，SVD是复杂矩阵的因式分解。对于给定的m * n矩阵M，存在分解使得M=UΣV，其中U和V是酉矩阵，Σ是对角矩阵。

实际上，PCA是SVD的一个简单应用。在计算机视觉中，第一个人脸识别算法使用PCA和SVD来将面部表示为"特征面"的线性组合，进行降维，然后通过简单的方法将面部匹配到身份，虽然现代方法更复杂，但很多方面仍然依赖于类似的技术。

10.独立成分分析（Independent Component Analysis，ICA）

ICA是一种统计技术，主要用于揭示随机变量、测量值或信号集中的隐藏因素。